
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Координаты вектора в пространстве
|
|
Базисом в пространстве называются три некомпланарных вектора  , взятые в определённом порядке (рис.1.32). Эти векторы
, взятые в определённом порядке (рис.1.32). Эти векторы  называются базисными.
называются базисными.

Пусть в пространстве задан базис  . Построим прямые
. Построим прямые  , содержащие базисные векторы
, содержащие базисные векторы  соответственно. Без ограничения общности можно считать, что эти прямые пересекаются в одной точке (в противном случае можно было взять любые пересекающиеся в одной точке прямые
соответственно. Без ограничения общности можно считать, что эти прямые пересекаются в одной точке (в противном случае можно было взять любые пересекающиеся в одной точке прямые  , параллельные прямым
, параллельные прямым  соответственно, поскольку проекции вектора на параллельные прямые равны (см. свойство 1 проекций в разд. 1.2.2)). Тогда любой вектор
соответственно, поскольку проекции вектора на параллельные прямые равны (см. свойство 1 проекций в разд. 1.2.2)). Тогда любой вектор 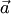 можно однозначно представить в виде суммы своих проекций:
можно однозначно представить в виде суммы своих проекций:  , где
, где  — векторы, принадлежащие прямым
— векторы, принадлежащие прямым  соответственно (см. п.2 теоремы 1.1). Раскладывая проекции
соответственно (см. п.2 теоремы 1.1). Раскладывая проекции  по базисам на соответствующих прямых (см. разд.1.3.1), находим:
по базисам на соответствующих прямых (см. разд.1.3.1), находим:  . Подставляя эти разложения в равенство
. Подставляя эти разложения в равенство  , получаем
, получаем

27)
Изоморфи́ зм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённойструктурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.
Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными. Классическим примером изоморфных систем могут служить множество  всех вещественных чисел с определённой на нём операцией сложения и множество
всех вещественных чисел с определённой на нём операцией сложения и множество  положительных вещественных чисел с заданной на нём операцией умножения. Отображение
положительных вещественных чисел с заданной на нём операцией умножения. Отображение 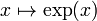 в этом случае является изоморфизмом.
в этом случае является изоморфизмом.