Подпространство

Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat (L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

§ ;

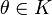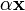§ для всякого вектора , вектор также принадлежал K, при любом ;

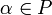§ для всяких векторов 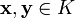, вектор 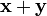также принадлежал K.

Последние два утверждения эквивалентны следующему:

§ для всяких векторов 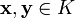, вектор 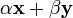также принадлежал K для любых .

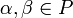В частности, пространство, состоящее из одного элемента {θ }, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.

[править]Свойства подпространств

§ Пересечение любого семейства подпространств — снова подпространство;

§ Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств определяется как множество, содержащее всевозможные суммы элементов K_i:

.

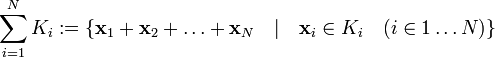В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.

Векторное пространство