Матрица перехода

Координаты вектора в базисе -- это коэффициенты разложения вектора по базису , где .

Пусть даны два базиса и , причем , , .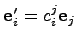

Определение. Матрица

-ый столбец которой составлен из координат вектора в базисе , называется матрицей перехода от базиса к . Имеем .

Лемма. Пусть -- базис, а и -- матрицы размера над полем , причем . Тогда .

Теорема. 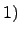Матрица перехода от базиса к невырождена.

Для любого базиса и любой невырожденной квадратной матрицы порядка 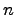существует и при том единственный базис с матрицей перехода , т.е. .

Теорема. Если -- матрица перехода от базиса к , то для любого вектора справедливо равенство , где и -- столбцы координат вектора в базисах и соответственно, т.е. .

Определение. Биекция линейного пространства 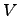над полем на линейное пространство над полем называется изоморфизмом линейных пространств, если для любых векторов и .

Следствие. Справедливы равенства , и . Если система линейна независима, то система тоже линейна независима. Отображение -- изоморфизм.

Определение. Два линейных пространства называются изоморфными, если существует изоморфизм одного пространства на другое.

Теорема. Два конечномерных пространства над полем изоморфны тогда и только тогда, когда .

Следствие. Любое 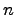-мерное векторное пространство 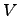изоморфно . Отображение определено так: .

30)

Определение

Пусть G — заданная группа и W — векторное пространство. Тогда представление группы G — это отображение, ставящее в соответствие каждому элементу невырожденное линейное преобразование причем выполняются свойства

Раздел математики, который изучает представления групп, называется теорией представлений (групп). Представление можно понимать как запись группы с помощью матриц или преобразований линейного пространства. Смысл использования представлений групп заключается в том, что задачи из теории групп сводятся к более наглядным задачам из линейной алгебры. Этим объясняется большая роль теории представлений в различных вопросах алгебры и других разделов математики. Например, одномерные представления симметрической группы S_n и знакопеременной группы A_n играют большую роль при доказательстве невозможности разрешения в радикалах алгебраического уравнения степени выше 4. В квантовой механике важную роль играют бесконечномерные (в которых векторное пространство — гильбертово) представления групп (в первую очередь, группы Лоренца).