Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Подпространство векторного пространства
|
|
Определение 2. Непустое множество векторов  векторного пространства
векторного пространства 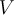 называется линейным подпространством 6), если:
называется линейным подпространством 6), если:
1.  для любых векторов
для любых векторов 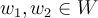 ;
;
2.  для всех
для всех  .
.
Определение 3. Коразмерностью 7) линейного подпространства  называется разность
называется разность  .
.
Определение 4. Подпространство, коразмерность которого равна 1, называется гиперплоскостью 8).
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:
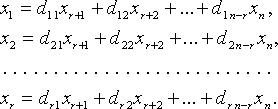
Тогда n - r линейно независимыми вектор-решениями будут:
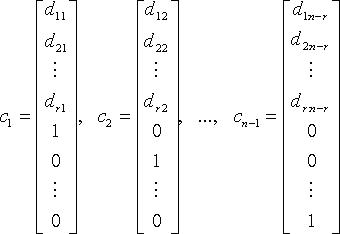
а любое другое решение является их линейной комбинацией. Вектор-решения 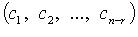 образуют нормированную фундаментальную систему.
образуют нормированную фундаментальную систему.
В линейном пространстве  множество решений однородной системы линейных уравнений образует подпространство размерности n - r;
множество решений однородной системы линейных уравнений образует подпространство размерности n - r; 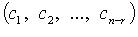 - базис этого подпространства.
- базис этого подпространства.
29)
Связь между базами. Объектом изучения являются для нас конечномерные линейные пространства. Понятно, что, изучая n-мерные линейные пространства, мы по существу изучаем то n-мерное векторное пространство строк, которое было введено еще в гл. 2. Однако раньше в этом пространстве была выделена одна база - а именно база, составленная из единичных векторов, т. е. векторов, у которых одна координата равна единице, а все остальные координаты равны нулю, - и все векторы пространства задавались строками их координат в этой базе; теперь же все базы пространства являются для нас равноправными.
Посмотрим, как много баз можно найти в n -мерном линейном пространстве и как эти базы связаны друг с другом.
Пусть в n -мерном линейном пространстве V заданы базы
e 1, e 2, …, e n (4)
и
e 1 ’, e 2 ’, …, e n ’ (5)
Каждый вектор базы (5), как и всякий вектор пространства V, однозначно записывается через базу (4),
 i=1, 2,..., п. (6)
i=1, 2,..., п. (6)
Матрица
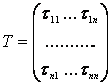
строки которой являются строками координат векторов (5) в базе (4), называется матрицей перехода от базы (4) к базе (5).
Связь между базами (4) и (5) и матрицей перехода Т можно записать, ввиду (6), в виде матричного равенства
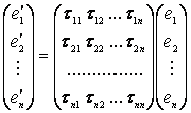 (7)
(7)
или, обозначая базы (4) и (5), записанные в столбец, соответственно через е и е', в виде
е'=Те.
С другой стороны, если Т' — матрица перехода от базы (5) к базе (4), то
e=T’e’
Отсюда
e=(Т’Т)e’,
e’=(ТТ’)e
т. е., ввиду линейной независимости баз е и е',
Т'Т=ТТ'=Е,
откуда
T’=T -1
Этим доказано, что матрица перехода от одной базы к другой всегда является невырожденной матрицей.
Всякая невырожденная квадратная матрица порядка п с действительными элементами служит матрицей перехода от данной базы п-мерного действительного линейного пространства к некоторой другой базе.
Пусть, в самом деле, дана база (4) и невырожденная матрица Т порядка п. Возьмем в качестве (5) систему векторов, для которых строки матрицы Т служат строками координат в базе (4); имеет место, следовательно, равенство (7). Векторы (5) линейно независимы— линейная зависимость между ними влекла бы за собой линейную зависимость строк матрицы Т в противоречие с ее невырожденностью. Поэтому система (5), как линейно независимая система, состоящая из п векторов, является базой нашего пространства, а матрица Т служит матрицей перехода от базы (4) к базе (5).
Мы видим, что в n-мерном линейном пространстве можно найти столь же много различных баз, как много существует различных невырожденных квадратных матриц порядка п. Правда, при этом две базы, состоящие из одних и тех же векторов, но записанных в различном порядке, считаются различными.
Ма́ трицей перехо́ да от базиса 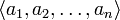 к базису
к базису  является матрица, столбцы которой — координаты разложения векторов
является матрица, столбцы которой — координаты разложения векторов  в базисе
в базисе 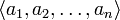 .
.
Обозначается