Определение

Определение 1. Пусть — некоторое поле. Абелева группа¹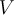⁾ называется векторным пространством ²⁾, или линейным пространством ³⁾ над полем , если задано отображение 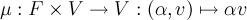, удовлетворяющее условиям:

1. для всех ;

2. 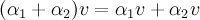для всех ;

3. для всех ;

4. 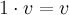для всех .

При этом элементы пространства 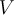называются векторами ⁴⁾, а операция — умножением на скаляр.

Замечание 1. Данное определение можно переформулировать в терминах модулей: левый унитарный модуль 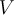над полем называется векторным пространством. Кроме того, в некоммутативной алгебре под векторным пространством понимают более широкий класс модулей, сохраняющий все основные свойства векторных пространств в их классическом понимании: левый унитарный модуль 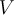над телом называется векторным пространством.

Пример 1. Нульмерное векторное пространство 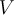состоит из одного элемента: .

Пример 2. 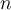- мерное координатное пространство над полем представляет собой декартово произведение 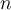множителей 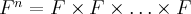. Элементы 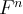записываются в виде векторов-строк 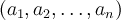⁵⁾. Операции сложения и умножения на скаляр определены покоординатно:

,
.

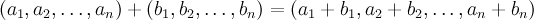Нулевым элементом является вектор 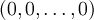, противоположным для 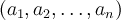служит вектор-строка .

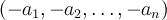Пример 3. Множество 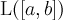функций, определенных на отрезке 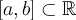и интегрируемых на нем по Лебегу, с поточечной операцией сложения , 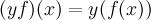является векторным пространством над полем действительных чисел.

Пример 4. Пусть 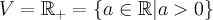. Введем на 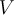операцию 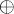по правилу и операцию умножения на скаляр 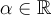по правилу 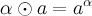. Нетрудно проверить, что 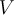с указанными операциями является векторным пространством над полем . Нейтральным элементом служит 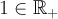.