
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка гипотезы об однородности.
|
|
Пусть проводится  независимых серий испытаний: в первой серии проводится
независимых серий испытаний: в первой серии проводится  независимых испытаний, в каждом из которых происходит в точности одно из событий
независимых испытаний, в каждом из которых происходит в точности одно из событий 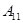 , …,
, …,  , во второй серии проводится
, во второй серии проводится 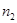 независимых испытаний, в каждом из которых происходит в точности одно из событий
независимых испытаний, в каждом из которых происходит в точности одно из событий 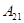 , …,
, …,  , и так далее, в
, и так далее, в  -ой серии проводится
-ой серии проводится  независимых испытаний, в каждом из которых происходит в точности одно из событий
независимых испытаний, в каждом из которых происходит в точности одно из событий  , …,
, …,  . Вероятности событий
. Вероятности событий  неизвестны. По результатам серии фиксируется количество
неизвестны. По результатам серии фиксируется количество  наступлений каждого события
наступлений каждого события  , и наблюдение представляет собой вектор
, и наблюдение представляет собой вектор  , функция распределения которого является произведением полиномиальных распределений
, функция распределения которого является произведением полиномиальных распределений  .
.
Основная гипотеза  заключается в том, что при фиксированном
заключается в том, что при фиксированном  и переменном
и переменном  события
события  имеют одинаковые вероятности, то есть выполняются равенства,
имеют одинаковые вероятности, то есть выполняются равенства,
 ,
,
…,
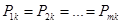 ,
,
или, что тоже самое, при фиксированном  и переменном
и переменном  вероятности
вероятности  при некоторых
при некоторых  , где вектор вероятностей
, где вектор вероятностей  играет роль параметра:
играет роль параметра:
 :
: 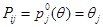 ,
,
 ,
,  .
.
Вероятность  , поэтому
, поэтому  не входит в вектор параметров
не входит в вектор параметров 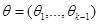 . Требуется предложить критерий проверки гипотезы
. Требуется предложить критерий проверки гипотезы  .
.
Для решения задачи используется статистика,
 ,
,
где вектор вероятностей  является МП-оценкой параметра
является МП-оценкой параметра 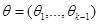 и
и  . Гипотеза
. Гипотеза  определяет функцию распределения наблюдения
определяет функцию распределения наблюдения  как полиномиальное распределение:
как полиномиальное распределение:
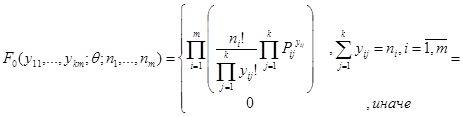
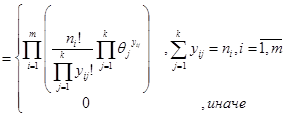 .
.
Таким образом, функция правдоподобия  и МП-оценка
и МП-оценка  доставляет максимальное значение функции
доставляет максимальное значение функции  (или минимальное значение функции
(или минимальное значение функции  ) при условии
) при условии 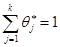 .
.