Практическая задача регрессионного анализа.

На практике совестное вероятностное распределение 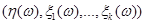редко бывает известно, тем не менее, в некоторых случаях можно вполне обоснованно предположить, что условное математическое ожидание является функцией определенного вида:

,

где – некоторый неизвестный числовой вектор.

Пусть случайная величина , тогда:

,

.

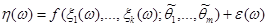В качестве исходных данных для задачи построения регрессии выступает наблюдение , в котором каждая случайная величина получена при условии, что , …, :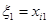

,

…
,

где – векторная случайная величина, – числовые значения (, ), – векторная случайная величина. Введем обозначение для матрицы числовых значений : .

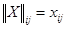Задача построения регрессии заключается в нахождении оценки неизвестного вектора параметров на основе наблюдения , например, в нахождении такого вектора параметров 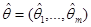, при котором среднеквадратичное отклонение :

.

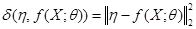
принимает наименьшее возможное значение:

.

Вектор в общем случае зависит от наблюдения , поэтому , вообще говоря, является некоторой векторной случайной величиной.