Определение характеристик сложных случайных величин.

Пусть 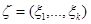– совокупность случайных величин с плотностью вероятности 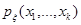, для которой известен метод получения реализаций, – некоторая известная функция и для случайной величины 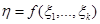требуется определить какие-либо характеристики, например, значение функции распределения в некоторой точке или моменты.

Значение функции распределения 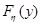случайной величины в точке определяется интегралом:

,

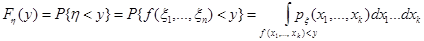где 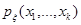– плотность вероятности вектора 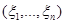. В общем случае, аналитическое вычисление кратного интеграла по области 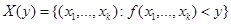может представлять определенные трудности, поэтому для приближенного вычисления используются методы статистических испытаний.

На основе случайного вектора образуем случайную величину:

.

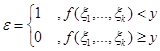Легко видеть, что математическое ожидание :

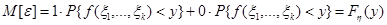
совпадает с неизвестной величиной 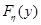, подлежащей определению. Пусть 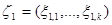, …, 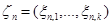– совокупность независимых случайных векторов, определим совокупность случайных величин , …, ,

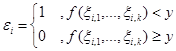
тогда:

.

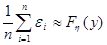Заметим, что величина 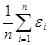совпадает с величиной эмпирической функции распределения 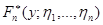в точке (величины ).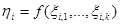

Предположим, требуется вычислить математическое ожидани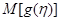е , где 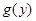заданная функция (например, 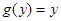, тогда 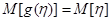– математическое ожидание , или 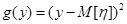, тогда 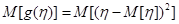– дисперсия ). Определим случайную величину:

,

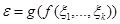тогда 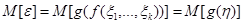. Пусть 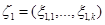, …, 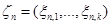– совокупность независимых случайных векторов, определим совокупность случайных величин , …, :

,

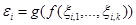тогда,

.
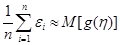