
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Помилки першого та другого роду.
|
|
Нехай дано вибірку  з невідомого розподілу
з невідомого розподілу  , и постовлена бінарна задача перевірки статистичних гіпотез:
, и постовлена бінарна задача перевірки статистичних гіпотез:

де H 0 — нульова гіпотеза, а H 1 — альтернативна гіпотеза. Припустимо, що заданий статистичний критерій
 ,
,
що зіставляє кожній реалізації вибірки  одну з гіпотез, які маємо. Тоді можливі чотири ситуації:
одну з гіпотез, які маємо. Тоді можливі чотири ситуації:
1.Розподіл  вибірки
вибірки 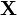 відповідає гіпотезі H 0, і вона точно визначена статистичним критерієм, тобто
відповідає гіпотезі H 0, і вона точно визначена статистичним критерієм, тобто  .
.
2.Розподіл  вибірки
вибірки 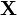 відповідає гіпотезі H 0, але вона невірно знехтувана статистичним критерієм, тобто
відповідає гіпотезі H 0, але вона невірно знехтувана статистичним критерієм, тобто  .
.
3.Розподіл  вибірки
вибірки 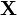 відповідає гіпотезі H 1, і вона точно визначена статистичним критерієм, тобто
відповідає гіпотезі H 1, і вона точно визначена статистичним критерієм, тобто  .
.
4.Розподіл  вибірки
вибірки 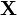 відповідає гіпотезі H 1, але вона невірно знехтувана статистичним критерієм, тобто
відповідає гіпотезі H 1, але вона невірно знехтувана статистичним критерієм, тобто  .
.
У другому і четвертому випадку говорять, що відбулася статистична помилка, і її називають похибкою першого і другого роду відповідно.
| Вірна гіпотеза | |||
| H 0 | H 1 | ||
| Результат застосування критерію | H 0 | H 0 вірно прийнята | H 0 невірно принята (Похибка другого роду) |
| H 1 | H 0 невірно знехтувана (Похибка першого роду) | H 0 вірно знехтувана |
Як видно з вищенаведеного визначення, похибки першого і другого роду є взаємно-симетричними, тобто якщо поміняти місцями гіпотези H 0 и H 1, то похибки першого роду перетворяться на похибки другого роду і навпаки. Проте, в більшості практичних ситуацій плутанини не відбувається, оскільки прийнято вважати, що нульова гіпотеза H 0 відповідає стану «за умовчанням» (природному, найбільш очікуваному стану речей) — наприклад, що обстежена людина здорова, або що проходить через рамку металлодетектора пасажир не має заборонених металевих предметів. Відповідно, альтернативна гіпотеза H 1 позначає протилежну ситуацію, яка зазвичай трактується як менш вірогідна, неординарна, така, що вимагає якої-небудь реакції.
З урахуванням цього похибку першого роду часто називають помилковою тривогою, помилковим спрацьовуванням — наприклад, аналіз крові показав наявність захворювання, хоча насправді людина здорова, або металлодетектор видав сигнал тривоги, спрацювавши на металеву пряжку ременя. Через можливості помилкових спрацьовувань не вдається повністю автоматизувати боротьбу з багатьма видами погроз. Як правило, вірогідність помилкового спрацьовування корелює з вірогідністю пропуску події (похибки другого роду). Тобто, чим чутливіша система, тим більше небезпечних подій вона детектує і, отже, запобігає. Але при підвищенні чутливості неминуче зростає і вірогідність помилкових спрацьовувань. Тому занадто чутливо (параноїдально) настроєна система захисту може звиродніти в свою протилежність і привести до того, що побічна шкода від неї перевищуватиме користь.
Відповідно, похибку другого роду іноді називають пропуском події — людина хвора, але аналіз крові цього не показав, або у пасажира є холодна зброя, але рамка металлодетектора його не виявила (наприклад, через те, що чутливість рамки відрегульована на виявлення тільки дуже масивних металевих предметів).
Ступінь чутливості системи захисту повинен бути компромісом між вірогідністю похибок першого і другого роду. Де саме знаходиться точка балансу, залежить від оцінки ризиків обох видів помилок.
Ймовірності похибок (рівень значущості і потужність)
Ймовірність похибки першого роду при перевірці статистичних гіпотез називають рівнем значущості і зазвичай позначають грецькою буквою α (звідси назва α -errors).
Ймовірність похибки другого роду не має якоїсь особливої загальноприйнятої назви, на папері позначається грецькою буквою β (звідси β -errors). Проте з цією величиною тісно зв'язана інша, що має велике статистичне значення — потужність критерію. Вона обчислюється за формулою (1 − β). Таким чином, чим вище потужність, тим менше вірогідність зробити похибку другого роду.
Обидві ці характеристики зазвичай обчислюються за допомогою так званої функції потужності критерію. Зокрема, ймовірність похибки першого роду є функцією потужності, обчисленою при нульовій гіпотезі. Для критеріїв, заснованих на вибірці фіксованого обсягу, ймовірність похибки другого роду є одиниця мінус функція потужності, обчислена в припущенні, що розподіл спостережень відповідає альтернативній гіпотезі. Для послідовних критеріїв це також вірно, якщо критерій зупиняється з ймовірністю одиниця (при даному розподілі з альтернативи).
У статистичних тестах зазвичай доводиться йти на компроміс між прийнятним рівнем похибок першого і другого роду. Часто для ухвалення рішення використовується порогове значення, яке може варіюватися з метою зробити тест строгішим або, навпаки, м'якшим. Цим пороговим значенням є рівень значущості, яким задаються при перевірці статистичних гіпотез. Наприклад, у разі металлодетектора підвищення чутливості приладу приведе до збільшення ризику похибки першого роду (помилкова тривога), а пониження чутливості — до збільшення ризику похибки другого роду (пропуск забороненого предмету).