Обратная матрица

Пусть дана квадратная матрица:

.

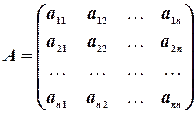Обозначим .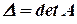

Квадратная матрица называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если .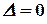

Квадратная матрица 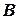называется обратной для квадратной матрицы того же порядка, если их произведени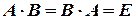е , где - единичная матрица того же порядка, что и матрицы и .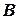

Теорема. Для того чтобы матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

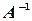Матрица, обратная матрице , обозначается через , так что . Обратная матрица вычисляется по формуле

,

где 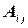- алгебраические дополнения элементов . Или

Таким образом, обратная матрица – это транспонированная матрица алгебраических дополнений, умноженная на коэффициент .

Вычисление обратной матрицы по этой формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП).

Любую неособенную матрицу путем ЭП только столбцов (или только строк) можно привести к единичной матрице .

Если совершенные над матрицей ЭП в том же порядке применить к единичной матрице , то в результате получится обратная матрица. Удобно совершать ЭП над матрицами и одновременно, записывая обе матрицы рядом через черту.

Замечание. Отметим, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

Пример 15. Для матрицы найти обратную ей матрицу.

Решение. Находим сначала детерминант матрицы (для этого прибавляем ко второму столбцу первый, а от третьего отнимаем первый, деленный на два):

значит, обратная матрица существует, и мы ее можем найти по формуле:

,

где ‑ алгебраические дополнения элементов исходной матрицы.

, _,

_{, ,}

_{, ,}

_{, ,}

Откуда

.

Пример 16. Методом элементарных преобразований найти обратную матрицу для матрицы: .

Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.

1. Поменяем местами первый и второй столбцы:

.

2. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на :

.

3. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на второй;

.

4. Прибавим третий столбец к первому и второму:

.

5. Умножим последний столбец на :

.

Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице . Итак,

.