Б. Формулы Крамера

Назовем столбцы матрицы следующим образом: первый столбец - 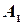, второй столбец - 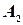, и т.д., последний столбец - .

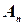Составим 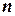дополнительных матриц:

, , …, ,

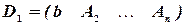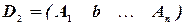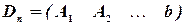и вычислим их определители и определитель исходной матрицы:

, , , …, .

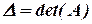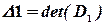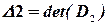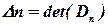Тогда значения неизвестных вычисляются по формулам Крамера:

, , …, .

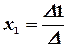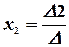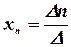Правило Крамера дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по вышеприведенным формулам.

Если главный определитель системы 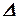и все вспомогательные определители 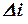равны нулю, то система имеет бесчисленное множество решений.

Если главный определитель системы 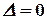, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Пример. Решить систему уравнений методом Крамера.

, .

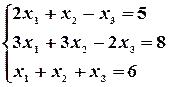
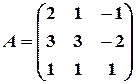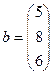Тогда

, , .

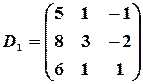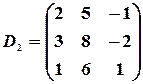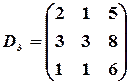Вычисляя определители этих матриц, получаем , , , .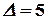

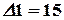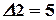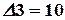И по формулам Крамера находим: 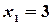, , .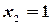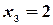