Факультеты химический, биоинженерии и биоинформатики. 1. 3. В инерциальной системе отсчёта частица движется по прямой, если сумма действующих на неё сил равна нулю

ВАРИАНТ 1

1.3. В инерциальной системе отсчёта частица движется по прямой, если сумма действующих на неё сил равна нулю. Следовательно, силы, действующие на протон со стороны электрического и магнитного поля, направлены в разные стороны и равны по величине. Из уравнения движения протона (второго закона Ньютона)

qE − qvB = 0

находим искомую скорость:

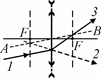
ной плоскости линз. Отложив такое же расстояние за плоскостью линз,

Факультеты химический, биоинженерии и биоинформатики

находим заднюю фокальную плоскость. Луч 3 пересекается с побочной оптической осью в точке пересечения её с этой фокальной плоскостью.

1.5. Из уравнения состояния идеального газа p = nkT следует, что давление газа p пропорционально произведению его абсолютной тем-

пературы T и концентрации молекул n. Здесь k – постоянная Больц-мана. По условию температура газа увеличилась в 2 раза. Когда полови-на двухатомных молекул распалась на атомы, частиц в сосуде стало в 1, 5 раза больше. Поскольку объем сосуда не изменился, концентрация частиц также возросла в 1, 5 раза. Ответ: давление газа увеличилось в

a = 3 раза.

1.6. Поскольку по условию сопротивлением воздуха можно пренебречь, при решении проще всего воспользоваться законом сохранения механи-ческой энергии системы «сосулька + Земля». За нулевой уровень отсче-та потенциальной энергии тяготения удобно выбрать горизонталь, про-ходящую через точку соударения с поверхностью крыши BC. Точка от-рыва B находится выше этого уровня на h = l sina, поэтому равенство механических энергий в моменты времени, когда сосулька находится в точке B и в точке касания с участком крыши BC можно записать так:

Отсюда нетрудно получить ответ: v 0 =

2 gl sina

n 2 − 1

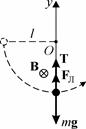
1.7. Выберем инерциальную систему отсчёта, связанную с Землей, направив координатную ось Oy вертикально вверх к точке подвеса нити. На шарик действуют три силы – сила тяжести m g, сила натяжения нити

рика при прохождении им нижней точки траектории в проекции на ось Oy:

Решения задач

тростремительное ускорение шарика равно:

Скорость шарика в нижней точке траектории легко найти из закона сохранения механической энергии:

Рис. 63

Решая совместно записанную систему уравнений, получаем ответ: T =3 mg − qB 2 gl.

1.8. При нормальном падении на дифракционную решетку плоскопа-раллельного пучка монохроматического света от лазера дифракционные максимумы располагаются симметрично относительно центрального (ну-левого) максимума. Угловое положение максимумов определяется ус-ловием:

d sin = m l,

где m – порядок дифракции. Поскольку угол дифракции не может пре-вышать 90° (sinf £ 1), то максимальный порядок доступного для на-

где символ [L] означает целую часть числа. По условию наблюдаются

всего k = 7 максимумов. Это означает, что в данном случае m max= 3. Следовательно, период решетки d > m maxl. Однако, период решетки

Факультеты химический, биоинженерии и биоинформатики

должен быть меньше, чем (m max+1)l, иначе будет наблюдаться меньше семи максимумов. Таким образом, период решетки лежит в диапазоне:

m maxl < d < (m max+1)l, т.е. 3l < d < 4l. Ответ: 1, 9 мкм < d < 2, 5 мкм.

1.9. Энергия электрического поля конденсатора равна

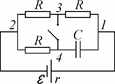Здесь U – разность потенциалов между обкладками конденсатора ем-костью C, а индексы 1 и 2 соответствуют исход-ному и замкнутому состоянию ключа K. Разность потенциалов U проще всего найти, если учесть, что она равна падению напряжения на параллель-ном с конденсатором однородном участке цепи, по которому протекает постоянный ток (исполь-

Рис. 64 зуя закон Ома для однородного участка цепи). При разомкнутом ключе (см. рис. 64) – это уча-

сток 1 − 3 − 2, имеющий сопротивление 2 R. По нижней ветви 1 − 4 − 2, включающей конденсатор, ток не течет. Поэтому сила тока, протекаю-щего по участку 1 − 3 − 2, определяется законом Ома для полной цепи:

а интересующая нас разность потенциалов равна:

После замыкания ключа полное сопротивление внешней цепи становит-ся равным 1, 5 R. Параллельно конденсатору теперь подключен участок 3 − 2 с сопротивлением R. Сила тока и разность потенциалов на этом

участке равны, соответственно:

Решения задач

Подставляя найденные значения разностей потенциалов в выражение для энергии конденсатора и беря отношение соответствующих величин, получаем ответ:

Отметим теперь, что импульс системы «шарик + клин» при соударении, очевидно, изменяется: до удара он был горизонтален, а после удара по-является вертикальная составляющая этого импульса, связанная с от-скочившим вверх шариком. Физическая причина этого изменения также понятна – в процессе соударения появляется дополнительная состав-ляющая внешней силы – силы реакции опоры. Однако горизонтальная составляющая импульса системы сохраняется, поскольку реакция гладкой опоры не имеет проекции на это направление. Следовательно,

mv 0= Mu.

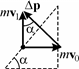Самый тонкий момент в решении этой задачи – сообра-зить, что вектор изменения импульса шарика ∆ p направ-

лен строго перпендикулярно наклонной поверхности кли-на. Эта поверхность также гладкая и импульс силы, дей-

ствующей на шарик со стороны клина в процессе удара,

не имеет касательной к этой поверхности составляю- Рис. 65 щей. Остается сделать аккуратный рисунок (см. рис.65) с указанием векторов импульса шарика до и после удара, а также вектора изменения

Факультеты химический, биоинженерии и биоинформатики

импульса шарика. Из рисунка видна связь модулей соответствующих импульсов:

Решая записанную систему уравнений, получаем ответ:

ctga =

M − m 7

M 8

ВАРИАНТ 2

2.3. Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре. Поэтому, исходя из представленного в условии задачи графика, сначала следует построить зависимость температуры газа от его объема (см. рис. 66).

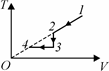
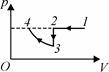Рис. 66 Рис. 67

Теперь нетрудно установить, что процесс 1 − 2 изобарный, 2 − 3 – изохор-ный, а 3 − 4 – изотермический. Искомая диаграмма представлена на рис. 67. Здесь учтено, что точки 1, 2 и 4 лежат на одной изобаре (давления газа в этих точках одинаково), а также качественно соблюдены пропорции при изменении объема в процессах 1 − 2 и 3 − 4. Участок 3–4 – отрезок ги-перболы.

2.4. Отметим прежде всего, что ультразвуковой вибратор – это кри-сталл, колеблющийся с ультразвуковой частотой, который может быть использован как генератор и как приёмник акустических волн. Обозна-чим через v скорость воздушного потока относительно лабораторной системы отсчёта, а через U скорость звука относительно воздушного потока, причём U > v. Используя закон сложения скоростей, запишем

Решения задач

1 2

2.5. Обозначим через угол преломления. По закону преломления

где n – показатель преломления вещества относительно воздуха. Абсо-лютный показатель преломления воздуха мало отличается от единицы. Поэтому n можно считать равным абсолютному показателю преломле-ния вещества. Учитывая, что по условию угол между отраженным и преломленным лучами прямой, и используя закон отражения, можно записать соотношение a +b = p/2. Отсюда следует, что sinb = cosa.

Тогда из закона преломления вытекает равенство: tga = n. Согласно волновой теории света

где c – скорость света в вакууме, v – скорость света в веществе. Ответ:

2.6. Эта задача является хорошей иллюстрацией применения закона Ома для неоднородного (содержащего ЭДС) участка цепи. Чтобы найти заряд q на пластинах конденсатора в предложенной схеме, необходимо

вначале определить разность потенциалов | 1− f2|= U между обклад-ками конденсатора. По определению электроёмкости конденсатора C она связана с абсолютной величиной заряда его обкладок равенством:

Факультеты химический, биоинженерии и биоинформатики

Поскольку конденсатор подключен к полюсам источника параллельно, искомую разность потенциалов можно найти, записав закон Ома для неоднородного участка цепи. Учитывая, что ток через источник проте-кает от положительного полюса к отрицательному (работа сторонних сил отрицательна), а сопротивление участка равно сопротивлению ис-точника r, имеем:

Отсюда f1− f2=E + Ir. Ответ: q = C (E + Ir) =1, 2× 10− 5Кл.

Замечание. Полезно построить график изменения потенциала

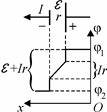
равна f1− f2=E + Ir. Приведенный анализ поведения потенциала на участке цепи, содержащем источник, помогает дать ответ ещё на один важный вопрос: что покажет вольтметр, подключенный к клеммам источника? Идеальный вольтметр в рассматриваемом случае (когда ток через источник течет от положительной клеммы к отрицательной) покажет напряжение U 1=E + Ir. В частности, такой случай реализует-ся, при зарядке аккумуляторов. Если ток через источник течет от отри-цательной клеммы к положительной, то вольтметр покажет напряже-ние U 2=E − Ir. Предлагаем обосновать этот результат самостоятельно, построив график зависимости потенциала вдоль участка цепи также и для этого случая.

Решения задач

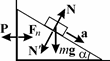2.7. Скольжение бруска вдоль наклонной поверхности клина проис-ходит под действием двух сил: силы тяжести m g и

силы реакции наклонной плоскости N, которая в

отсутствии трения перпендикулярна плоскости (см. рис. 69). По второму закону Ньютона для бру-ска в проекциях на направления вдоль наклонной плоскости и перпендикулярное к ней имеем:

Рис. 69

ma = mg sina, 0 = N − mg cosa.

2.8. Исходя из указанной в условии задачи зависимости между темпе-ратурой и объемом газа, делаем заключение, что температура газа квадра-тично зависит от его объема:

T ~ V 2.

В соответствии с объединённым газовым законом параметры заданного количества идеального газа в любом процессе связаны друг с другом соот-ношением:

Факультеты химический, биоинженерии и биоинформатики

pV = const.

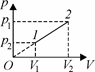Из этих выражений следует, что в рассматриваемом процессе давление газа растет пропорционально объему (p ~ V). Для опреде-

ления работы газа удобно представить процесс его рас-ширения на pV– диаграмме (см. рис. 70). Работа числен-но равна «площади под графиком» зависимости p от

Поскольку точки 1 и 2 лежат на прямой, проходящей через начало коорди-

Согласно уравнению состояния идеального газа, pV = n RT,

где n – число молей газа. Поэтому искомая работа равна

2.9. Линейное увеличение k изображения предмета, даваемого линзой – это отношение линейного размера изображения к линейному размеру предмета. Как легко убедиться, оно равно отношению расстояния f от

Решения задач

Расстояние между изображением предмета и рассеивающей линзой можно найти с помощью формулы линзы:

2.10. Прежде всего, отметим, что момент максимального растяжения пружины соответствует нижнему положению груза в процессе его вер-тикальных колебаний. В этот момент пружина растянута на величину

∆ x = x 0 + A,

где A – амплитуда колебаний грузика. Здесь учтено важное обстоя-тельство, что в положении равновесия системы пружина уже растянута. Величина этого растяжения x 0 соответствует равенству сил тяжести и упругости:

0 = mg − kx 0.

Факультеты химический, биоинженерии и биоинформатики

Чтобы найти эту величину, необходимо, таким образом, найти параметры A и k. Амплитуда колебаний A, очевидно равна половине расстояния S между двумя крайними положениями грузика:

Жёсткость пружины связана с периодом колебаний грузика T хорошо известным соотношением:

В свою очередь период колебаний равен удвоенному времени движения грузика между двумя крайними положениями:

T = 2t.

Решая записанную систему уравнений, получаем ответ:

E п = 8p2t2» 0, 2 Дж.

ВАРИАНТ 3

3.3. По закону Фарадея ЭДС индукции E i равна скорости измене-ния магнитного потока F через поверхность, ограниченную проводящим контуром:

Рис. 71 ся в промежутке от 12 с до 16 с. В промежутке

Решения задач

ках графика ЭДС равна нулю, т.к. изменения магнитного потока не про-исходит. Соответствующая зависимость представлена графически на рис. 71.

3.4. При движении брусков из начального положения в конечное потенциальная энергия каждого из них изменяется на одну и ту же ве-личину. В соответствии с законом сохранения энергии часть потенци-альной энергии каждого из брусков перейдет в кинетическую энергию, а часть израсходуется на работу против силы трения. Брусок, который был пущен вниз, пройдет до основания наклонной плоскости меньший путь, чем другой брусок. Следовательно, для этого бруска работа про-тив силы трения будет меньше, чем для бруска, пущенного вверх. От-вет: у основания наклонной плоскости бó льшую скорость будет иметь брусок, который пущен вниз.

3.5. В исходном положении поршня силы, действующие на него со стороны воздуха, находящегося внутри и снаружи цилиндра, уравнове-шены. Каждая из этих сил по модулю равна

При вытаскивании поршня из цилиндра давление воздуха в цилиндре уменьшается, и к поршню приходится прикладывать все увеличиваю-щуюся силу. Когда поршень находится у открытого конца цилиндра, эта сила максимальна. В этом положении поршня объем воздуха в цилинд-ре увеличится в два раза, а его давление по закону Бойля-Мариотта уменьшится в два раза. В два раза уменьшится также сила давления на поршень со стороны воздуха в цилиндре, а сила атмосферного давления останется прежней. Поэтому к поршню должна быть приложена сила, направленная наружу и не меньшая, чем

Факультеты химический, биоинженерии и биоинформатики

3.6. При разомкнутом ключе батарею можно представить в виде двух параллельно соединенных участков, в каждом из которых после-довательно соединены конденсаторы с электроемкостями C и 3 C. В

При замкнутом ключе батарею можно представить в виде двух последо-вательно соединенных участков, в каждом из которых конденсаторы C и 3 C соединены параллельно. В этом случае ёмкость батареи C 2 = 2 C. Ответ: при замыкании ключа ёмкость увеличилась в

3.7. Количество теплоты, выделяемое нагревателем за промежуток времени t,

За вычетом тепловых потерь на плавление льда пойдет количество теп-лоты

С другой стороны, для того чтобы расплавить массу льда m требуется количество теплоты

Решения задач

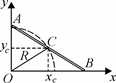3.8. При решении задачи главное – это установить, по какой траек-тории движется центр стержня (точка С). Для

этого следует сделать аккуратный чертеж (см. рис. 72) и убедиться из равенства прямоугольных треугольников (например, ∆ OxcC и ∆ CxcB), что расстояние ОС – постоянная величина, равная половине длины стержня. Следовательно, траек-

с центром в точке O. Путь, проходимый точкой C в рассматриваемом движении стержня, равен четверти длины этой окружности. Ответ:

диода, то количество теплоты, выделившейся на этом резисторе за вре-мя t, было бы равно

При включенном в цепь диоде ток через резистор отличен от нуля толь-ко в течение половины каждого периода. Поэтому на резисторе выделя-ется вдвое меньшее количество теплоты:

Аналогично, количество теплоты, выделившееся на резисторе R 2, рав-но

Q 2= 4 R 2.

Общее количество теплоты, выделившееся на обоих резисторах,

Факультеты химический, биоинженерии и биоинформатики

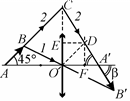
Рис. 73 поэтому изображение стержня располагается на прямой, имеющей такой же наклон к главной оптической оси линзы, что и луч 2 после преломления в линзе. Из рисунка видно, что

Кроме того, из подобия ∆ OCA ¢ и ∆ CED следует, что

Поскольку по условию Ð AOC = 45°, справедливы равенства: OC = d, ED = F, EC = d − F. Решая записанную систему уравнений, находим

ВАРИАНТ 4

4.3. Приведенная на рис. 14 зависимость координаты материальной точки от времени описывается выражением

x = x maxcos t,

Решения задач

ний. Проекция скорости точки на ось Ox равна производной от коорди-наты по времени:

Значения x max= 2 см и T = 8 с определяются из графика. Ответ: v max»1, 57 см/с.

4.4. Задача решается очень просто, если знать особенности использо-вания собирающей линзы в качестве лупы. Для того чтобы получить уве-личенное мнимое изображение предмета, его располагают вблизи фокаль-ной плоскости линзы между линзой и фокусом. Записывая формулу линзы, имеем:

Это равенство легко преобразуется в квадратное уравнение относительно фокусного расстояния линзы

F 2− xF − xf = 0, корни которого имеют вид:

Для собирающей линзы следует выбрать положительный корень. Фокусное расстояние линзы равно F = 5 см, а её оптическая сила D = 1= 20 дптр.

Факультеты химический, биоинженерии и биоинформатики

4.5. Обозначим через a угол, который образует крыша с горизонта-лью. В отсутствии трения тела скользят вдоль крыши (наклонной плос-

t =

2 S 2 L 4 L

a g cosa sina g sin2a

Время скольжения минимально при максимальном значении sin2a, которое достигается при a = 45°. Ответ: H = L = 2, 5 м.

p 0 S + Mg + 2 mg = pS.

Отсюда находим искомую величину

4.7. Рассмотрим электрическую схему, описанную в условии (см. рис. 74). В процессе разрядки конденсатора после замыкания ключа K через резисторы протекает ток, сила которого меняется во времени, по-степенно убывая. Однако в любой момент времени через резисторы те-

Решения задач

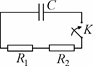чет одинаковый ток. Согласно закону Джоуля–Ленца мощности, выде-ляющиеся в резисторах, равны, соответственно

N 2 R 2

не зависит от времени. Поэтому такое же отношение Рис. 74 справедливо и для количеств теплоты, выделившихся в конденсаторах за время разрядки конденсатора:

При этом полное количество выделившейся теплоты равно энергии, запасенной в конденсаторе:

Из этих соотношений находим ответ: