
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. МЕХАНИКА. I.1. При упругом ударе о наклонную плоскость составляющая ско-рости шарика, параллельная плоскости
|
|
 I.1. При упругом ударе о наклонную плоскость составляющая ско-рости шарика, параллельная плоскости, не изменяется, а составляющая, перпендикулярная плоскости, оставаясь
I.1. При упругом ударе о наклонную плоскость составляющая ско-рости шарика, параллельная плоскости, не изменяется, а составляющая, перпендикулярная плоскости, оставаясь
той же по величине, меняет направление на противопо-ложное. Следовательно, после удара шарик отскочит от наклонной плоскости со скоростью v 0 под углом = p − 2a к горизонту. Кинематические уравнения дви-
жения шарика в системе координат, изображенной на рис. 78, имеют вид:

В точке падения шарика на плоскость выполняются соотношения: x = l, y = l tga.
Исключая из записанных выражений время, получаем ответ:
v 0=
gl
2cos2(p − 2a)[tga + tg(p − 2a)]
gl cosa 2sina |cos2a |
 I.2. Траектория мяча, соответствующая максимальной скорости, удовлетворяющей условию задачи, изображена на рис. 79. При упругом ударе о стенку вертикальная составляющая скорости мяча не изменяет-ся, а горизонтальная, оставаясь той же по величине, меняет направление
I.2. Траектория мяча, соответствующая максимальной скорости, удовлетворяющей условию задачи, изображена на рис. 79. При упругом ударе о стенку вертикальная составляющая скорости мяча не изменяет-ся, а горизонтальная, оставаясь той же по величине, меняет направление
| |||||
| |||||
|

Факультет ВМиК
 на противоположное. Зависимость высоты мяча над поверхностью зем-ли имеет вид:
на противоположное. Зависимость высоты мяча над поверхностью зем-ли имеет вид:


Время полета мяча до ограждения
|
|
 0 v 0cosa
0 v 0cosa
 Рис. 79 Мяч не перелетит через ограждение, если y (t 0) £ h. Исключая из записанных выражений время, получаем ответ:
Рис. 79 Мяч не перелетит через ограждение, если y (t 0) £ h. Исключая из записанных выражений время, получаем ответ:
L + l 0 cosa
|

|
Рис. 80
эффициент сопротивления воды. По второму закону Ньютона имеем: F =b v 0. Из рисунка видно, что F = F cosJ, где J – угол, который
|
 cosJ = l 0− v 0 t.
cosJ = l 0− v 0 t.
(l 0− v 0 t)2+ h 2
 Объединяя записанные равенства, получаем:
Объединяя записанные равенства, получаем:
F = b v 0
(l 0− v 0 t)2+ h 2 l 0− v 0 t
 | |||||||||||
| |||||||||||


 Решения задач
Решения задач
F =b v 0 l 2+ h 2, откуда b v 0= F 0
l 0.
l 2+ h 2
Ответ: F (t) = F l 0
l 2+ h 2
(l 0− v 0 t)2+ h 2 l 0− v 0 t

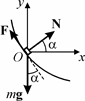 I.4. Брусок движется по горизонтальной окружности под действием сил, изображенных на рис. 81, где m g – сила тяжести,
I.4. Брусок движется по горизонтальной окружности под действием сил, изображенных на рис. 81, где m g – сила тяжести,
N – нормальная составляющая силы реакции сферы, F – сила трения. В проекциях на оси OX и OY непод-
вижной координатной системы имеем:
m w 2 R cosa = N cosa − F sina,
F cosa + N sina − mg = 0. Рис. 81 Исключая отсюда N, находим
F = m cosa(g − w 2 R sina).
Если угловая скорость вращения сферы такова, что w 2 R sina > g, то сила трения направлена противоположно. В общем случае ответ имеет вид: F = m cosa | g − w 2 R sina |.
I.5. На правую чашу весов, заполненную водой до краев, действует сила
F = Mg + N,
Факультет ВМиК
 где M = Sh – масса воды в этой чаше, N – сила давления падающих
где M = Sh – масса воды в этой чаше, N – сила давления падающих
капель дождя. Поскольку соударение капель с водой, находящейся в чаше, является неупругим, по второму закону Ньютона имеем:
∆ m × v = (N − ∆ m × g)∆ t,

|
время ∆ t. Отсюда


|

|


|

|
|
|
|
I.6. В момент, когда достигается максимальное сжатие пружины, скорость бруска обращается в нуль. По закону изменения механической энергии имеем:

|

|
|
|
|
|

|
|
|
|
|
|
 | |||
 | |||

Решения задач
 Объединяя записанные выражения, получаем квадратное уравнение относительно ∆ l:
Объединяя записанные выражения, получаем квадратное уравнение относительно ∆ l:



|
|
|
|
|
Поскольку по условию задачи предоставленный самому себе брусок

|

|
|
|
|
|
2 k (H − l sina) ü
|
 I.7. Шарики находятся в равновесии под действием сил, модули и направления которых изображены на рис. 82, где
I.7. Шарики находятся в равновесии под действием сил, модули и направления которых изображены на рис. 82, где
mg – модуль силы тяжести. В проекции на гори-
зонтальное и вертикальное направления условия равновесия шариков имеют вид:
|
|
|
|
Отсюда вытекают следующие равенства:
|
|
|

|
|

|
Факультет ВМиК
 I.9. Стакан будет находиться под водой в безразличном равновесии при выполнении условия
I.9. Стакан будет находиться под водой в безразличном равновесии при выполнении условия
mg = r Vg,

|
Мариотта
|
где p = p 0+r gh – давление воды на глубине h. Объединяя записанные выражения, находим

|
При меньшей глубине погружения предоставленный самому себе ста-кан будет всплывать. Наоборот, при увеличении глубины погружения стакан начнет опускаться вниз, так как с ростом давления воды вытал-

|
*I.9. Пусть p – давление, создаваемое насосом, v – скорость воды в шланге. Согласно уравнению Бернулли,

|

|
|
|

|
Решения задач




|
|
|
|
|
|
|
|
|
 I.10. По закону сложения ускорений ускорение свободного падения относительно системы отсчета, связанной с вагоном,
I.10. По закону сложения ускорений ускорение свободного падения относительно системы отсчета, связанной с вагоном,
g 1 = g − a. Из рис. 83 видно, что модуль этого ускоре-


|
|
мальный угол отклонения маятника от вертикали составит 2a. Как
видно из рисунка, h = l (1− cos2a) = 2 l sin2 a. Используя формулу


|
|
|
|