
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Theory of Errors
|
|
LABORATORY WORKS
Instructions of laboratory works arrangement
LABORATORY WORK consists of the following stages:
— study the work instructions and corresponding theoretical material;
— write a report on the work;
— be admitted to carry out the work;
— carry out experimental measurements;
— process results of measurements and enter them into the report;
— present the laboratory work to the teacher.
A LAB REPORT consists of the following parts: 1. The purpose and tasks of the work; 2. Theoretical information; 3. Devices and equipment; 4. Measurement method and deduction of formulas for calculation; 5. Tables of measurements and calculations; 6. Processing the results of measurements, evaluation of errors and drawing graphs; 7. Record of the results and the errors; 8. Conclusions.
In conclusion it is necessary to estimate the results in terms of laws of physics, to evaluate the accuracy of measurements and specify the cause of errors.
Theory of Errors
Classification of measurements and errors
MEASUREMENT of physical quantities is the purpose of each laboratory work. Measurement is comparison of some physical quantity with the known one taken for a unit of measurement by way of physical experiment. As a result, it is established how many times the measured quantity is bigger or smaller than the unit of measurement. Measurement methods are divided into two basic types: direct and indirect.
Measurement is direct if the magnitude of physical quantity is directly determined during an experiment.
Measurement is indirect if the required quantity is calculated through the dependence between this quantity and those determined by direct measurements using corresponding formulas or laws.
ERRORS show accuracy of measured values. Absolute error Δ x is the difference between measured x and true X values of physical quantity Δ x = x – X. The absolute error has the same unit of measurement as the measured quantity. The measured value х can be either greater or smaller than the true value X, therefore an absolute error can be both positive and negative. But the absolute error does not show accuracy of measurement as it is not compared to the measured value. Accuracy of measurement is characterized by a relative (fractional) error.
Fractional error ε is determined by the ratio of the absolute error to the true value of measuring quantity and is usually expressed in percents. As true value X is not known precisely, the average value is taken as the true one
 .
.
Errors are divided into three basic types depending on their source.
Systematic error is a component of the total error of measurement, being constant or dependently variable during repeated measurements of a quantity. This type of error arises if the measuring device is off-tuned. The same occurs in case of improper method of measuring. This error is decreased by using more precise and properly adjusted device. But it cannot be decreased up to zero.
A part of systematic error which cannot be avoided however perfect is the device has the name of instrumental error. This error depends on precision of the measuring device only. It can be determined if the device accuracy class is known. The instrumental error of any simple measuring device (ruler, household thermometer, stop watch etc.) is equal to half of the least scale factor of the device.
Random error is a component of total error changing a little in a casual way if the same measurement is repeated. To diminish a random error influence, it is necessary to repeat the measurement as many times as possible.
Gross error is a measurement error, which essentially exceeds the error expected at present conditions. Gross error causes are strong external factors, operator’s oversight, and devices in disrepair or their improper application. If we came to a conclusion, that measurement results contain gross errors the results are to be rejected. After that, it is desirable to establish the cause of a mistake, to correct malfunctions and lacks and to repeat measurements all over again.
Errors of direct measurements
DIRECT measurements cannot be carried out with absolute accuracy because of a lot of reasons, such as lack of devices accuracy, imperfectness of methods of measurement, influence of external conditions, observer’s inexperience and so on. Therefore the purpose of measurement is not merely to find a value but evaluate its deviation from the true one. It means to specify the accuracy guaranteed by the given measurement in other words its error.
Assume that we have conducted several measurements of certain physical quantity x, the number of measurements is equal to n. When the number of experiments approaches infinity, obtained values and absolute errors of these values as well obey the normal distribution law (Gaussian distribution). The typical normal distribution curve of absolute error f (D x) is shown in Fig. 5.1. The vertical axis represents division of number of measurements D ni which have deviation D xi value to total number of measurements n. The distribution function is determined by the expression
 ,
,
where s is a standard deviation; s2 is a variance of error.

 The peak value of distribution function means D x = 0, so this measurement is the most probable (average) value or else arithmetic mean of all the values < x > of measured quantity:
The peak value of distribution function means D x = 0, so this measurement is the most probable (average) value or else arithmetic mean of all the values < x > of measured quantity:
 .
.
The root-mean-square error of n experiments is equal to
 ,
,
where  is the absolute error (random deviation) of every experiment.
is the absolute error (random deviation) of every experiment.
When the number of experiments approaches infinity the arithmetic mean tends to the true value and the root-mean-square error tends to standard deviation:

 .
.
Hatched area size in Fig. 5.1 is proportional to probability that the true value of measured quantity belongs to the interval
 .
.
THE INTERVAL AND PROBABILITY are named confidence interval and confidence probability. Reducing D x leads to reducing probability and vice versa. The choice of confidence probability value depends on the purpose of measurements. In most practical cases, the value equal to 0, 95 is used.
If we have finite number of experiments, the arithmetic mean would be nearly the same as the true value but not equal to it, i.e. an average value has its own error  .
.
Root-mean-square error of arithmetic mean is equal to
 or
or  .
.
It is easy to notice that on the way to reduce an error of series of measurements by 2 times, the quantity of measurements needs to be increased by 4 times, for reduction of an error by 3 times, the quantity of measurements ought to be increased by 9 times and so on. This dependence is expression of the increase in accuracy with the increase of quantity of measurements law. But it is executed only when the random error is bigger than the instrumental one and completely determines the common error of the measurements.
All these conclusions are correct only on condition of a very big number of measurements, in practice this quantity seldom exceeds 10, and it is 3-5 measurements more often. Reducing experiments number leads to the increase in difference between  and s, consequently, confidence probability will decrease. The confidence probability for such quantities of measurements will be very small; therefore it is necessity to increase it artificially, expanding a confidence interval. For realisation of the interval extension, the correction factor (Student’s coefficient) is applied. Connection between quantity of measurements, confidence probability and width of a confidence interval was established in 1908 by the English mathematician Goset. He published the works under the pseudonym “Student”.
and s, consequently, confidence probability will decrease. The confidence probability for such quantities of measurements will be very small; therefore it is necessity to increase it artificially, expanding a confidence interval. For realisation of the interval extension, the correction factor (Student’s coefficient) is applied. Connection between quantity of measurements, confidence probability and width of a confidence interval was established in 1908 by the English mathematician Goset. He published the works under the pseudonym “Student”.
STUDENT’S COEFFICIENT magnitude (t – coefficient) depends on a number of experiments n and confidence probability P value and we can find the coefficient in the corresponding table. It is necessary to multiply Root-mean-square error of arithmetic mean by the coefficient to receive the size of a confidence interval at desirable confidence probability.

Table of Student’s coefficient t
| п | Confidence probability Р | ||
| 0, 90 | 0, 95 | 0, 99 | |
| 2, 92 2, 35 2, 13 2, 02 1, 94 1, 89 1, 86 1, 83 | 4, 30 3, 18 2, 78 2, 57 2, 45 2, 36 2, 31 2, 26 | 9, 92 5, 84 4, 60 4, 03 3, 71 3, 50 3, 36 3, 25 |
THE RULES of definition of the total error:
1. If random error considerably smaller than instrumental (at least 5 times), the instrumental error is taken as total error.
2. If random error essentially exceeds the instrumental one, we should increase the number of measurements to reduce the random error.
3. If these errors have the same number position, we are to find the total absolute error as shown below:
THE ORDER of error determination of quantity x, if both random and instrumental errors have influence, is the following:
1. Determine an arithmetic mean value of all measurement results as the most close one to true value of quantity x:
 (5.1)
(5.1)
2. Calculate random deviation Δ x i of every obtained result:
Δ xi = xi –  (5.2)
(5.2)
3. Determine a root-mean-square error of the arithmetic mean value:
 (5.3)
(5.3)
4. Use the Student’s coefficients table to determine t- coefficient for the chosen confidence probability and the number of experiments n.
5. Calculate the absolute random error D x r of direct measurements:  (5.4)
(5.4)
6. Determine total absolute error D x, as the geometric sum of random error D x r and instrumental error  :
:
 . (5.5)
. (5.5)
7. The final measurement result of quantity x is expressed as follows:
 (5.6)
(5.6)
Indirect measurement error estimation rules
INDIRECT MEASUREMENT ERRORS evaluation rules can be obtained only by means of the errors mathematical theory and differential calculus methods. The error of indirect measurement depends on the velocity of function change while the argument varies i.e.
 ,
, 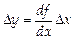 ,
,
where D y and D x are absolute indirect and direct measurement errors.
Therefore, if the function is presented as
 ,
,
then the measurement error of quantity y is defined by the expression

 ,
,
where  , …
, …  are partial derivatives of function in respect to independent arguments.
are partial derivatives of function in respect to independent arguments.
Fractional error is defined as follows
 .
.
We get from the previous expressions
 .
.
According to differentiation rules, we have
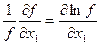 ; …
; …  .
.
Thus, we obtain expression for fractional error of indirect measurement. It looks as follows:
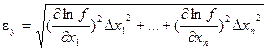 .
.
Let’s apply this expression to the case where the required quantity is connected with the results of direct measurements by dependence occurring in physics.
 , where A and k are constant values, which can be integer or fraction, negative or positive. Take the logarithm of the function.
, where A and k are constant values, which can be integer or fraction, negative or positive. Take the logarithm of the function.
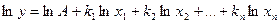 .
.
Calculate partial derivatives using the table of derivatives
 ;
; 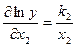 ;
; 
Using the expression for a fractional error, one can obtain the formula for fractional error calculation of the function.
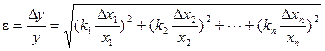 .
.