Задачі для самостійного розв’язання

1. Довести, що чотирикутник з вершинами А(3, 2, -3), В(2, 4, 6), С(8, 3, 4), D(9, 1, -5) є паралелограм.

2. Показати, що точки А(3, 4, 1), В(1, 0, -1) і С(-2, -6, -4) лежать на одній прямій.

3. Дані точки А(-3, 6, 1) і В(7, -9, -4). Знайти координати точок С, D, Е, i F, які ділять відрізок АВ на п’ять рівних частин.

4. Знайти координати кінців P і Q відрізка, який точками М(3, 1, 3) і N(6, -1, 1) розділений на три рівні частини.

Відповіді: 3. С(-1, 3, 0), D(1, 0, -1), E(3, -3, -2), F(5, -6, -3)

P(0, 3, 5), Q(9, -3, -1).

2.7. Кут між векторами. Проекція вектора на вісь. Властивості проекцій

1. Кут між векторами. Нехай задані ненульові вектори . Зведемо ці вектори до спільної точки О і в напрямках векторів проведемо з точки О промені (див. рис. 15).

Менший з кутів, які утворені цими променями називається кутом між векторами і позначається .

Кут між вектором 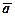і нульовим вектором не означається.

Очевидно, що якщо , то ; Якщо ж то .

Вправи. 1). Знайти , , .

2). Нехай . Знайти .

Рис. 15

3). Розглянемо рівнобедренний прямокутний трикутник АВС, де . Знайти

Відповіді:

2. Проєкцію вектора 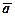на вісь 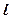(позначається ) називається довжина відрізка, який сполучає проекції на цю вісь початку і кінця вектора, взята зі знаком «+», якщо кут між вектором і віссю гострий і знаком «-», якщо цей кут тупий (рис. 16).

Очевидно, що коли , то =0, і навпаки.

Основні властивості проекцій:

1. = (рис. 16);

2. = (рис. 17);

3. = + (рис. 18).

Властивість 3 виконується для суми скінченного числа векторів.