Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Составление корреляционной решетки
|
|
Заключается в группировке данных в сопряженные между собой взвешенные ряды. Перед началом группировки следует выбрать независимую переменную (аргумент “X”) и зависимую переменную (функцию “Y”). Выбор аргумента и функции является довольно условным, так как иногда сложно установить, какой признак является причиной взаимного влияния, а какой следствием. Например, в корреляционной связи диаметра и высоты ствола, длины подземной части сеянцев и высоты их надземной части тот и другой признак парной связи может служить и аргументом, и функцией.
В случае затруднений в выборе аргумента и функции ориентируются по корреляционному отношению прямой и обратной связи двух коррелируемых признаков. Если обратное корреляционное отношение больше прямого, то за аргумент принимают другой признак. Вариационный ряд, принимаемый за аргумент, располагается в горизонтальном ряду графика, а принятый за функцию – в вертикальном.
Необходимо иметь ввиду, что корреляционные связи, не слишком отклоняющиеся от прямолинейных, могут быть удовлетворительно оценены коэффициентом корреляции, вычисление которого значительно проще вычисления корреляционного отношения; допустимая степень отклонения корреляционной связи от прямолинейной определяется с помощью критерия криволинейности.
Рассмотрим особенности парной корреляционной связи на примере измерений длины надземной и подземной частей однолетних сеянцев сосны, произведенных студентами лесохозяйственного факультета на лесопитомнике учебно-опытного лесхоза УГЛТУ. Было измерено 100 сеянцев, результаты занесены в корреляционную решетку (Табл. 12).
Таблица 12
Корреляционная решетка распределения подземной части (x) и надземной части (y) однолетних сеянцев сосны и расчет показателей для вычисления коэффициента их корреляции
| Высота сеянцев, см. | Длина подземной части сеянцев, см. | ||||||||||||
| Итого ny | ay | ayny | a2y | a2yny | |||||||||
| +6 | |||||||||||||
| –5 | +5 | ||||||||||||
| — | +4 | — | |||||||||||
| +3 | |||||||||||||
| –6 | +2 | ||||||||||||
| –3 | –2 | –2 | +1 | ||||||||||
| – 4 | – 6 | – 6 | –1 | –20 | |||||||||
| –10 | –12 | –8 | –2 | –50 | |||||||||
| Итого nx | – | –12 | – | ||||||||||
| ax | –3 | –2 | –1 | +1 | +2 | +3 | +4 | – | |||||
| ax nx | –21 | –38 | –16 | ||||||||||
| a2x | – | ||||||||||||
| a2x nx | |||||||||||||
| nxy·ax· ay | –2 |
После построения корреляционной решетки необходимо установить степень криволинейности изучаемой связи. Это можно сделать визуально, построив на корреляционной решетке график эмпирической зависимости, или аналитическим путем. Построенный от руки график свидетельствует о наличии кривизны связи, хотя и слабо выраженной. В этом случае допускается вычисление коэффициента корреляции вместо корреляционного отношения, так как, во-первых, значительно упрощаются вычисления, и, во-вторых, значение коэффициента корреляции будет незначительно отличаться от значения корреляционного отношения и достаточно точно оценивать тесноту связи изучаемых признаков.
При проведении вычислений произвольно выбирают условную средину горизонтального и вертикального рядов распределения. Условная средина должна быть по возможности ближе к средине ряда и совпадать с клеткой, в которой содержится наибольшая частота. Условные отклонения (в нашем примере по горизонтали ах изменяются от – 3 до + 4, по вертикали ау от + 6 до – 2). Далее условные отклонения умножают на частоты горизонтального и вертикального рядов, затем квадраты условных отклонений также умножают на частоты; полученные произведения суммируют.
Находят произведения условных отклонений между собой и на совместную для них частоту:
В первом столбце: (–3)·1·2= –6; (–3)·1·1= –3; (–3)·2·(–1) = 6;
(–3)·2·(–2)=12. И так по каждому столбцу. Полученные произведения суммируют в столбцах с соблюдением знаков, получая значения nxy·ax· ay, которые суммируют (в нашем примере сумма = 90).
В итоге вычислений получают суммы по строкам (х) и по столбцам (у):
∑ nx = Nx = 100; ∑ ax nx = 15; ∑ a2x nx = 367
∑ ny = Ny = 100; ∑ ay ny = –2; ∑ a2y ny = 302
∑ nxy·ax· ay = 90.
Далее находят стандартное отклонение горизонтального и вертикального коррелируемых рядов распределения по формуле (__):
σ х = 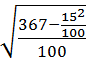 =
= 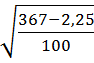 = 1, 910
= 1, 910
σ у = 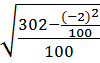 =
= 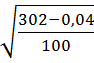 = 1, 738
= 1, 738
Коэффициент корреляции находят по формуле:
rxy = 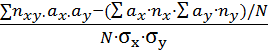 (44)
(44)
rxy 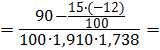
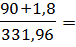 0, 276
0, 276
Ошибка достоверности коэффициента корреляции определяется по формуле:
t = 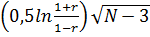 , (45)
, (45)
где t – критерий Стьюдента при числе степеней свободы У=N-2=
= 100 – 2 = 98.
t= 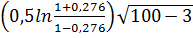 = (0, 5 ln 1, 767)·9, 849 =
= (0, 5 ln 1, 767)·9, 849 =
Объем выборки, достаточный для достоверности коэффициента корреляции, определяют по таблице 13П (Зайцева). На уровне значимости 0, 05 коэффициент корреляции 0, 277 достоверен при объеме выборки N, равном 50 (в нашем примере N = 100, следовательно, r = 0, 276 статистически достоверен).
Полученное значение коэффициента корреляции 0, 276 свидетельствует о слабой связи длины корней и высоты надземной части однолетних сеянцев сосны – лишь 27, 7% числа признаков (факторов) являются общими для длины корней и высоты надземной части сеянцев. Возведя коэффициент корреляции в квадрат, получают коэффициент детерминации r2, свидетельствующий о силе связи, о взаимообусловленности изменчивости двух показателей.
r2=0, 2762=0, 077=7, 7%. Только 7, 7% изменчивости высоты надземной части однолетних сеянцев сосны вызываются (обуславливаются) изменчивостью длины их корневой системы; остальная доля изменчивости обусловлена действием других, неизвестных факторов.
Коэффициент детерминации является более важным показателем связи в сравнении с коэффициентом корреляции.
Таблица 13
Объем выборки, достаточный для достоверности коэффициента корреляции на трех доверительных уровнях (по Г.Н. Зайцеву, 1984)