
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Совместное вычисление коэффициента корреляции и корреляционного отношения между взвешенными рядами
|
|
Совместное вычисление производят в случае, когда требуется дать количественную оценку степени криволинейности корреляционной связи, при этом определяют коэффициент детерминации r2 и точки эмпирической линии (табл. 13).
Для вычисления в табл. 13 составляют корреляционную решетку, суммируют частоты по столбцам (nx) и по строкам (nу). Условные отклонения ах и ау берутся от начала рядов, начиная с 0. Далее в столбцах получают суммы произведений частот на соответствующие им условные отклонения у (для первого столбца: 1 · 4 + 1 · 3 + 1 · 2 + 2 · 1 + 2 · 0 = 11). Полученные суммы произведений ∑ f·ay возводят в квадрат и делят на сумму частот в столбце: (∑ f·ay)·nx =112/7=17, 29, и т.д.
Необходимо получить точки корреляционной связи (регрессии). Для этого вначале суммы произведений частот на ау делят на соответствующие им в столбцах nx: для первого столбца ∑ f·ay/ nx=11/7=1, 57, и т.д.
Каждое из полученных значений умножают на величину классового интервала k (у нас k = 1) и к каждому полученному значению прибавляют минимальное значение ряда У (в нашем примере оно равно 4): 1, 57 · 1 + 4 = 5, 57, и т.д.
Таблица 13
Расчет показателей для совместного вычисления коэффициента корреляции и корреляционного отношения
| Х У | ∑ ny | ay | ∑ ny ay | ∑ ny a2y | ||||||||
| — | ||||||||||||
| ∑ nx | ||||||||||||
| ∑ f·ay | ||||||||||||
| (∑ f·ay)2/nx | 17, 29 | 23, 21 | 60, 61 | 29, 45 | 64, 22 | 97, 32 | 32, 67 | 64, 00 | 388, 22 | |||
| ax | ||||||||||||
| (∑ f·ay)/nx | 1, 57 | 1, 11 | 1, 94 | 1, 64 | 1, 89 | 2, 26 | 2, 33 | 4, 00 | ||||
| y/x | 5, 57 | 5, 11 | 5, 94 | 5, 64 | 5, 89 | 6, 26 | 6, 33 | 8, 00 | ||||
| ∑ nx·ax | ||||||||||||
| ∑ nx·a2x | ||||||||||||
| ∑ ax(∑ f·ay) |
Здесь f – частота, n – сумма частот, а – условное отклонение, N – число наблюдений.
Полученные значения 5, 57; 5, 11; 5, 94 и т.д.являются точками регрессии у/x (у по х). С использованием точек строится эмпирическая линия регрессии (рис.13).
Суммы частот в столбцах nx умножают на условные отклонения:
7 · 02 + 19 · 12 + 16 · 22 ...+ 4 · 72 = 315
Далее получают сумму nx· a2x:
7 · 02 + 19 · 12 + 16 · 22 +…+ 4 · 72 = 1357. Аналогично этим действиям получают суммы ny ay и ny a2y:
∑ ny ay = 25 · 0 + 20 · 1 + 27 · 2 +…+ 1 · 8 = 188
∑ ny a2y= 25 · 02 + 20 · 12 + 27 · 22 +…+ 1 · 82 = 654
Далее получают сумму ах·∑ f · ay:
∑ (ах·∑ f · ay) = 0 · 11 + 1 · 21 + 2 · 31 +…+ 7 · 16 = 684
Используя полученные в таблице суммы, рассчитывают коэффициент корреляции (r) и корреляционное отношение (η).
Коэффициент корреляции вычисляется по формуле:
r= 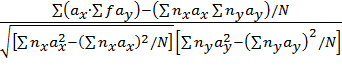 (46)
(46)
r= 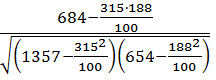 =
= 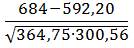 =
= 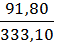 = 0, 276
= 0, 276
Корреляционное отношение вычисляется через его квадрат по формуле:
η 2 = 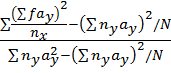 (47)
(47)
η 2 = 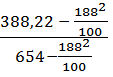 =
= 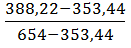 =
= 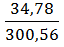 = 0, 116
= 0, 116
Отсюда η =  = 0, 340
= 0, 340
Оценку достоверности коэффициента детерминации r 2 производят по критерию Фишера F.
Оценка степени криволинейности связи осуществляется несколькими способами. Наиболее простые из них два способа:
а) η 2 у/x – r 2 ≥ 0, 1 (48)
Связь считается криволинейной, если разность квадратов η 2 и r 2 равна или превышает 0, 1.
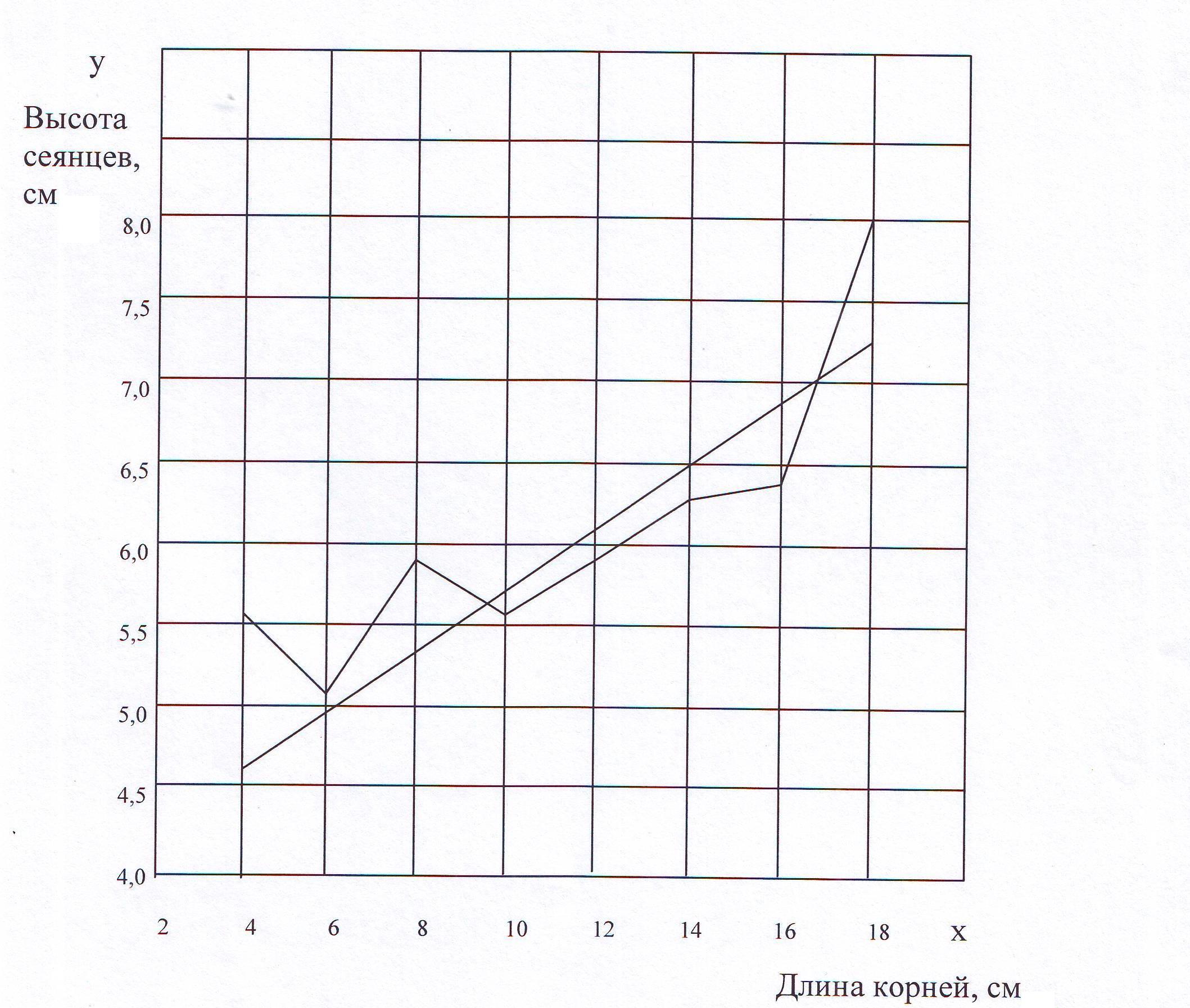
Рис. 13. Эмпирическая и теоретическая линии связи высоты однолетних сеянцев сосны (у) и длины их корневых систем (х).
В нашем примере показатель криволинейности равен 0, 3402 –0, 2762 = 0, 040, следовательно, связь не является криволинейной.
б) N (η 2 у/x – r 2) ≥ 11, 37, (49)
где 11, 37 – критерий криволинейности Блэкмана.
В нашем примере 100 · (0, 3402 – 0, 2762) = 100 · 0, 040 = 4 < 11, 37.
С помощью критерия Блэкмана подтверждена прямолинейность связи высоты надземной части однолетних сеянцев сосны с длиной их корневых систем (рис. 13).
В заключение отметим некоторые особенности, имеющие важное значение для анализа корреляционной связи, результаты которого получены в нашем примере:
Коэффициент корреляции, рассчитанный двумя способами, имеет одно и то же значение (r = 0, 276).
Предпочтение следует отдать второму способу совместного вычисления коэффициента корреляции и корреляционного отношения, так как этот способ позволяет: 1) определить ординаты связи и построить эмпирический график регрессионной связи; 2) определить степень кривизны связи; 3) рассчитать коэффициент детерминации и корреляционное отношение; 4) оценить уровень статистической достоверности коэффициента детерминации (r2) прямолинейной связи.
Не подтвердилось высказанное первоначальное мнение о наличии криволинейной зависимости высоты однолетних сеянцев сосны от длины их корневой системы.