
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корреляция рангов
|
|
Корреляция рангов применяется в случае, когда коррелируемые признаки могут быть расположены в определенном порядке по возрастающим (или убывающим) номерам или рангам. Ранг указывает место, которое занимает данная единица совокупности среди других единиц. Если некоторые из единиц совокупности оказываются в отношении рассматриваемого признака одинаковыми, то ранг всех этих единиц принимается равным среднему из соответствующих номеров.
Рассмотрим порядок расчета рангового показателя Спирмэна на примере измеренных диаметров и высот стволов модельных деревьев (Табл. 14).
ρ =1–  =
= 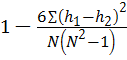 , (49)
, (49)
где 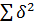 – сумма квадратов попарных разностей рангов.
– сумма квадратов попарных разностей рангов.
ρ =1–  =
=  = 1– 0, 33 = 0, 67
= 1– 0, 33 = 0, 67
Как и коэффициент корреляции, показатель ранговой корреляции изменяется в пределах – 1 + 1.
Критическое значение показателя корреляции рангов на 5% уровне значимости вычисляется по формуле
ρ = 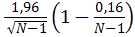
ρ = 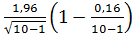 =
=  = 0, 653 · 0, 982 = 0, 64 (50)
= 0, 653 · 0, 982 = 0, 64 (50)
Вычисленный показатель 0, 67 больше критического значения 0, 64, следовательно, показатель ранговой корреляции достоверен на 5% уровне значимости.
Таблица 14
Вычисление показателей ранговой корреляции
| N/N n/n | Д, см Х1 | Н, м Х2 | h1 | h2 | h1- h2 | (h1- h2)2 |
| 25, 5 | 26, 5 | –3 | ||||
| 25, 0 | 26, 7 | –1 | ||||
| 24, 5 | 26, 1 | 3, 5 | –1, 5 | 2, 25 | ||
| 24, 0 | 28, 5 | +3 | ||||
| 24, 5 | 28, 6 | 3, 5 | +2, 5 | 6, 25 | ||
| 20, 0 | 24, 6 | +4 | ||||
| 20, 5 | 22, 0 | 8, 5 | –1, 5 | 2, 25 | ||
| 20, 8 | 24, 4 | |||||
| 20, 5 | 22, 3 | 8, 5 | +0, 5 | 0, 25 | ||
| 21, 0 | 22, 1 | –3 | ||||
| Сумма | – | – | –10+10 |