
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная регрессия
|
|
Она характеризует наиболее простой и распространенный тип зависимости, выраженный формулой
у = а·х + b, (__)
где а – размерный коэффициент, характеризующий скорость изменения функции у по мере изменения аргумента х, то есть
а = (у2 – у1) · (х2 – х1) (рис.__); b – значение у при х = 0.
Линейная связь может быть как положительной, так и отрицательной, когда соответственно коэффициент а > 0 и коэффициент корреляции r > 0 или а < 0 и r < 0 (рис.__).

Рис. 8. Линейная регрессия (уравнение прямой):
а – угловой коэффициент, характеризующий скорость изменения «у» при изменении «х»;
б – значение «у» при «х» = 0;
r – коэффициент кореляции.
Для вычисления коэффициентов уравнения прямой связи заполняют таблицы 15 и 16, вычисление производят с использованием уравнений (1) и (2) с последующей оценкой достоверности полученного уравнения прямой связи коррелируемых признаков.
Таблица 15
Расчет показателей для вычисления уравнения связи длины корневых систем (х) и высоты сеянцев (у)
| х у | n | х/у | ||||||||
| 12, 00 | ||||||||||
| 12, 67 | ||||||||||
| – | – | |||||||||
| 15, 50 | ||||||||||
| 11, 20 | ||||||||||
| 11, 20 | ||||||||||
| 9, 78 | ||||||||||
| 9, 60 | ||||||||||
| 9, 52 | ||||||||||
| n | ||||||||||
| y/x | 4, 43 | 5, 11 | 5, 94 | 5, 64 | 5, 89 | 6, 26 | 6, 33 | 8, 00 |
Таблица 16
Расчет показателей для вычисления уравнения связи длины корней (х) и высоты сеянцев (у)
| х | у | х2 | у · х | у/ | у/-y | (у/-y)2 |
| 8, 00 | 144, 00 | 7, 26 | –0, 74 | 0, 548 | ||
| 6, 33 | 101, 28 | 6, 88 | 0, 55 | 0, 302 | ||
| 6, 26 | 87, 64 | 6, 50 | 0, 24 | 0, 058 | ||
| 5, 89 | 70, 68 | 6, 12 | 0, 23 | 0, 053 | ||
| 5, 64 | 56, 40 | 5, 74 | 0, 10 | 0, 010 | ||
| 5, 94 | 47, 52 | 5, 36 | –0, 58 | 0, 336 | ||
| 5, 11 | 30, 66 | 4, 98 | –0, 13 | 0, 017 | ||
| 4, 43 | 17, 72 | 4, 60 | 0, 17 | 0, 029 | ||
| 47, 6 | 555, 90 | 47, 44 | –0, 16 | 1, 353 |
8 а0 + 88 а1 = 47, 6
88 а0 + 1136 а1 = 555, 9
_ 88 а0 + 1136 а1 = 555, 9
88 а0 + 968 а1 = 523, 6
168 а1 = 32, 3
а1 =  = 0, 1923; а0 вычисляется, исходя из уравнения (1);
= 0, 1923; а0 вычисляется, исходя из уравнения (1);
а0 =  =
=  =
= 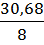 = 3, 84
= 3, 84
Уравнение регрессии принимает вид:
у = а0 + а1х = 3, 84 + 0, 1923  х
х
Ошибку уравнения регрессии вычисляют по формуле:
myx= 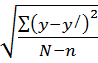 , (51)
, (51)
где myx – ошибка уравнения регрессии,
у – эмпирические значения функции,
у / – теоретические значения функции,
N – число точек эмпирической линии регрессии, n – число коэффициентов уравнения, включая свободный член.
myx=  = ± 0, 47
= ± 0, 47
Таким образом высоту сеянцев можно вычислить по формуле
у = 3, 84 + 0, 1923х с ошибкой ± 0, 47
На основании рассчитанных частот у / (табл. 16) строят график прямолинейной регрессии (рис. 13).
Точка пересеченных линий регрессии с осью ординат у = а0 = 3, 84.
Основным параметром прямолинейной регрессии является а1, поэтому рекомендуется оценить достоверность его отличия от нуля; степень достоверности коэффициента а1 отражает наличие или отсутствие корреляционной связи между признаками. Оценка достоверности производится по t – критерию Стьюдента по формуле:
t = 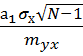 , (55)
, (55)
где t – величина критерия Стьюдента,
а1 – коэффициент при аргументе в уравнении прямой линии,
 – стандартное отклонение ряда аргумента,
– стандартное отклонение ряда аргумента,
 ошибка уравнения,
ошибка уравнения,
N – объем выборки (число классов).
t =  =
=  = 1, 06
= 1, 06 
Вычисление  представляется читателю. Если вычисленная величина t-критерия меньше табличной, то связь между х, у и значение а1, достоверны. Табличное значение t-критерия на 5% уровне значимости при числе степеней свободы у = N – 2 составляет:
представляется читателю. Если вычисленная величина t-критерия меньше табличной, то связь между х, у и значение а1, достоверны. Табличное значение t-критерия на 5% уровне значимости при числе степеней свободы у = N – 2 составляет:
N 10 20 30 40 50 60 70 80 90 100 200
t 1, 46 1, 27 1, 20 1, 15 1, 11 1, 08 1, 06 1, 04 1, 03 1, 02 0, 95.
Второй способ вычисления уравнения коэффициентов х0 и а1 прямой связи применяется, если известны коэффициент корреляции r и стандартные отклонения  коррелируемых рядов. Вычисление ведется по формуле:
коррелируемых рядов. Вычисление ведется по формуле:
а1 = rxy  (53)
(53)
Коэффициент а0 вычисляют по использованному выше уравнению (1), когда было найдено значение а0 = 3, 84.
Выше рассмотрен порядок оценки тесноты парной прямолинейной и криволинейной связи с помощью коэффициента корреляции r, корреляционного отношения η и показателя силы связи (взаимообусловленности изменчивости, детерминации) r2 и порядок вычисления уравнения прямолинейной регрессии у = а0 + а1х.