Теоретичне обґрунтування

Визначення сплайн-функції. Застосування моделей у вигляді сплайн-функцій доречне тоді, коли процес змін передбачає структурні зміни у різних областях вхідних змінних. Важливим моментом, який істотно впливає на спосіб побудови моделі, є тип переходу від одногорежиму до іншого. Виділяють дві ситуації:

1. Модельований процес неперервний і перехід з режиму на режим відбувається без різких коливань.

2. Природа екологічного процесу є такою, що переходи від режиму до режиму є стрибкоподібними.

Сплайн-функції передбачають плавний перехід.

Використання моделей процесів стану навколишнього середовища у вигляді сплайн-функцій доцільне в ситуаціях, коли зміна одного показника, зумовлена зміною іншого, і ця залежність не має різких коливань і розривів у розвитку.

Для розв’язання нашої задачі нам знадобиться параболічний сплайн.

Визначення. Мережею називається множина точок осі абсцис ∆ = (К₀, К₁, …, К_l), кожна з (l + 1)≥ 3 точок К_{і, j} є [0; 1], називається вузлом.

У₀, у₁, …, у_l – набір відповідних значень ординат.

Отож, параболічним сплайном над ∆, що інтерполює набір у, називається функція f_∆ (К), яка відповідає таким вимогам:

1) f_∆ (К) та її перша похідна неперервна на [К₀, К_l];

2) f_∆ (К) на інтервалі [К_j-1, К_j], j є [1; l] збігається із деяким многочленом, що є не більшим другого ступеню;

3) f_∆ (К) = у_j, j є [0; l].

Схематичний графічний вигляд сплайн-функції “відносна врожайність – коефіцієнт вологозабезпеченості”

у/уmax		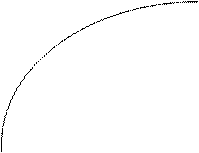						В	2А
				С
1, 0
			∆
0, 5	М	l
0				D1			D2		D3
				0, 5				1, 0	К

1 – лінійна залежність

2 – обвідна крива

Метод послідовної сплайн-апроксимації. Відповідно до визначення, подамо даний метод для намальованого схематичного графіку.

Як із нього видно, основні вимоги є такими:

1) ∆ = (К₀, К₁, К₂, К₃).

2) f₃(К) в області D₃ - лінійна та сполучає точки В та А;

3) на відрізку D₂, коли К є D₂, f₂(К) – квадратична, що плавно у точці В переходить у лінійну f₃(К);

4) f₁(К) у точці С плавно переходить у f₂(К);

5) точку М можна знаходити з умови, що f₁(К) оптимально апроксимує дані спостереження – точки К^і в області D₁ (за методом найменших квадратів).

Виходячи з вимог до функції f(К), легко побачити, що в області D₃ f₃(К)=1 при К є [К₂, К₃]; в області D₂ невідомі коефіцієнти функції f₂(К) знаходимо із умов:

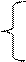а₀ + а₁ К₁ + а₂ К₁² = у/у^max | _{К1 = С}

а₀ + а₁ К₂ + а₂ К₂² = 1 (формула 1)

а₀ + 2 а₂ К₂ = 0

Знайдену у такий спосіб функцію f₂(К) можна поширити на область D₁ (на основі ідентифікації виразу для f₁(К)). Даний вираз можна знайти із умови сполучення у точці К=К_l, тобто неперервності сплайн-функції та її першої похідної:

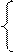f₂(К)=f₁(К), при К=К₁;

(формула 2)

f ^’₂(К)=f ^’₁(К), при К=К₁,

а також із системи умовних рівнянь Гаусса:

b₀ + b_l К_i + b₂ К_i² = (у/у^max) K_і є D_l. (формула 3)

На основі рівнянь формули 2 визначаються невідомі параметри b₀, b_l як функції третього коефіцієнта b₂ і підставляються у систему формули 3. Із цієї системи рівнянь коефіцієнт b₂ знаходиться за методом найменших квадратів або за методом середніх.

Запропонований підхід до ідентифікації сплайн-функції можна узагальнити послідовною добудовою сплайна у областях D₂, D₃ із використанням умовних рівнянь. У деяких випадках, після нанесення на графік точок (у/у^max, К)_і, значення абсцис і ординат мережі ∆ можна встановлювати за графіком, а сплайн-функцію визначати за допомогою теорії інтерполяції.