Операции над множествами

Продолжая описание методов получения новых множеств из уже существующих, мы опишем два метода, при помощи которых из двух множеств строится новое множество. Эти так называемые операции над множествами в некоторых отношениях аналогичны операциям сложения и умножения целых чисел. Объединение (соединение, сумма) множеств А и В (обозначается через А U В; А U В читается как «объединение А и В» или «А чашка В») есть, множество всех предметов, которые являются элементами множества А или В; иными словами,

А U В = { х | х Î А или х Î В).

Здесь подразумевается неисключающий смысл слова «или»1.

Таким образом, по определению х Î А U В тогда и только тогда, когда х есть элемент хотя бы одного из множеств А и В. Например,

{1, 2, 3} U {1, 3, 4} = {1, 2, 3, 4}.

Пересечение (произведение) множеств А и В (обозначается через А Ç В;

А Ç В читается как «пересечение А и В» или «А крышка В») есть множество всех предметов, являющихся элементами обоих мно­жеств А и В; иными словами:

А U В = { х | х Î А и х Î В).

Таким образом, по определению х Î А Ç В тогда и только тогда когда х Î А и х Î В. Например,

{1, 2, 3} Ç {1, 3, 4} = {1, 3}.

Предоставляем читателю в качестве упражнения доказать, что для всякой пары множеств А и В имеют место следующие включения:

Æ Í А Ç В Í А Í А U В.

Два множества А и В называются непересекающимися (или расчле­ненными), если А Ç В =Æ, и пересекающимися, если А Ç В ¹ Æ. Система множеств называется расчлененной, если любая пара ее различных эле­ментов является непересекающейся. Разбиением множества X мы будем называть такую расчлененную систему Aнепустых и различных под­множеств множества X, что каждый элемент множества X является в то же время элементом некоторого (а следовательно, в точности одного) элемента системы A. Например, {{1, 2}, {3}, {4, 5}} есть раз­биение множества {1, 2, 3, 4, 5}.

Следующая операция — операция перехода к дополнению — позволяет образовать новое множество из одного ранее существовавшего множе­ства. Абсолютно дополнение множества А (обозначается через Â)—это не что иное, как множество { х | х Î А }. Относительное дополнение мно­жества А до множества X — это множество XÇ Â; оно обычно обозна­чается через X — А, что читается как «X минус А». Таким образом, X — А есть сокращение для

{ х Î х ç х Ï А },

т. е. для множества тех элементов множества X, которые не являются элементами множества А.

Симметрическая разность множеств А и В, обозначаемая через А + В, определяется следующим образом:

A + B = (A-B) U (B-A).

Эта операция1 коммутативна [A + В = В + А] и ассоциативна [(А+В)+ С = А+(В+С)]. Кроме того, А+А = Æ и А + Æ = А. Доказательства этих утверждений предоставляются читателю.

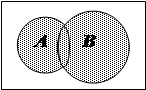
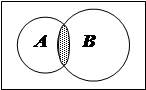
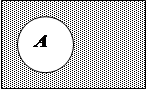
Если все рассматриваемые в ходе какого-либо рассуждения мно­жества являются подмножествами некоторого множества U, то это мно­жество U называют универсальным множеством (для этого рассуждения2). Например, для элементарной арифметики универсальным множеством служит Z, а для аналитической геометрии плоскости—множество всех упорядоченных пар действительных чисел. Для графической иллюстра­ции отношений, которые могут иметь место между подмножествами какого-либо универсального множества U, часто используют так назы­ваемые диаграммы Венна. Диаграмма Венна представляет собой схема­тическое изображение множеств в виде точечных множеств: универсаль­ное множество U изображается множеством точек некоторого прямо­угольника, а его подмножество А — в виде круга или какой-нибудь другой простой области внутри этого прямоугольника3. Дополнение множества А (до U), которое мы можем, не опасаясь двусмысленности, обозначать через Â, изображается в таком случае той частью прямо­угольника, которая лежит за пределами круга, изображающего А (рис. 1). Если изобразить таким образом какие-нибудь - множества А и В, являющиеся подмножествами множества U, то множества А Ç В и А U В изображаются областями, заштрихованными, соответственно, на рисунках 2 и 3. Непересекающиеся множества изображаются неперекрывающимися областями, а включение множеств соответствует тому обстоятельству, что одна из областей на диаграмме Венна целиком лежит внутри дру­гой. Построение диаграммы Венна для сложного выражения, составлен­ного из нескольких множеств посредством объединения, пересечения,

дополнения и включения, осуществляется комбинированием описанных способов построения диаграмм для этих составных частей. Диаграммы Венна применяются главным образом для упрощения некоторого дан­ного сложного выражения или совокупности условий на подмножества универсального множества. Ниже мы приведем три простых примера такого рода.

		Рис, 2. A Ç B заштриховано		Рис. 3. А U В заштриховано
	Рис. 1. Ā заштриховано

Во многих случаях такие диаграммы оказываются недоста­точными, но их использование все же может помочь при освоении алгеб­раического подхода, развиваемого в следующем параграфе.