
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры. 1.Пусть А и B — два таких множества, что А - В = В - A=Æ.Можно ли выразить отношение между А и В более простым образом?
|
|
| Рис. 6 |
1. Пусть А и B — два таких множества, что А - В = В - A= Æ.Можно ли выразить отношение между А и В более простым образом?
 | |||||
 | |||||
 |
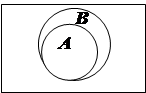
| Рис. 4 |
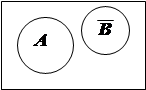
| Рис. 5 |


 Поскольку А – В = Æ означает, что А Ç В = Æ, области, представляющие А и В на диаграмме Венна (рис. 4), не перекрываются. Очевидно, В = В, так что мы получаем А Í В (рис. 5). И обратно, если А Í В, то, очевидно, А – В = Æ. Мы приходим к выводу, что А – В = Æ равносильно А Í В. Поменяв ролями А и В, мы получим, что В – А = Æ равносильно ВÍ А. Таким образом, заданные отношения между А и В равносильны тому, что А Í В и В Í А, т. е. А = В.
Поскольку А – В = Æ означает, что А Ç В = Æ, области, представляющие А и В на диаграмме Венна (рис. 4), не перекрываются. Очевидно, В = В, так что мы получаем А Í В (рис. 5). И обратно, если А Í В, то, очевидно, А – В = Æ. Мы приходим к выводу, что А – В = Æ равносильно А Í В. Поменяв ролями А и В, мы получим, что В – А = Æ равносильно ВÍ А. Таким образом, заданные отношения между А и В равносильны тому, что А Í В и В Í А, т. е. А = В.
2. Рассмотрим вопрос, можно ли указать три таких подмножества А, В и С универсального множества U, для которых одновременно имели бы место следующие соотношения:
С ¹ Æ, А Ç В ¹ Æ, А Ç С = Æ, (А Ç В) – С = Æ.
Из второго условия вытекает, что А и В пересекаются, из чего, кстати, следует, что оба они непусты. Согласно примеру 1 четвертое условие равносильно тому, что A Ç B Í C, из чего видно, что первое условие является излишним. С помощью диаграммы Венна легко убедиться, что А и С пересекаются, т. е. что второе и четвертое условия противоречат третьему. Следовательно, множеств, одновременно удовлетворяющих всем приведенным условиям, не существует.
3. Пусть F, G и L— такие подмножества множества U, что
F Í G, G Ç L Í F, L Ç F = Æ.
Можно ли на самом деле найти такие множества F, G и L, которые удовлетворяли бы этой совокупности условий? Диаграмма Венна (рис. 6) иллюстрирует только первое и третье условия. Но теперь из второго условия следует, что L и G не могут пересекаться, так что G Ç L = Æ. С другой стороны, если F Í G и
G Ç L = Æ, то выполняются все заданные условия. Таким образом, данная система условий может быть сведена к более простой: F Í G и G Ç L = Æ.
1 Впрочем, это относится не ко всем математикам даже и того времени. См. ниже, главу III, особенно § 3.9.— Прим. перев
1 Речь идет о так называемых антиномиях (противоречиях) теории множеств; см. ниже, §§ 1.2, 3.3 и 3.9.— Прим. перев
2 Насколько в действительности убедительны ссылки на «обычность» наивных теоретико-множественных методов, читатель более квалифицированно сможет судить после чтения последних параграфов главы III.— Прим. перев
1 И тем не менее, как отметил выше автор, именно это делал Кантор, а вслед за ним—большинство математиков. Речь идет, таким образом, о том, что, рассматривая в математике множества, элементы которых «даже теоретически нельзя собрать в за конченную совокупность», мы отвлекаемся от этой невозможности. Подробнее об этой так называемой абстракции актуальной бесконечности см., например, в соответствующей статье из первого тома «Философской энциклопедии» (М., I960).— Прим. перев.
2 Примеры: множество букв древнейшего алфавита ближайшей к Земле из существующих во Вселенной цивилизаций; множество людей, погибших в троянскую войну; множество возгласов «бис!» на послезавтрашнем концерте Рихтера... Читатель легко продолжит список.— Прим. перев.
1 Употребителен также термин принцип экстенсиональности.— Прим. перев;
1 В оригинале — formula (формула); в переводе мы предпочли воспользоваться более подходящим (и употребительным) для данной цели термином «форма», тем более, что слову «формула» ниже (начиная с § 2.3) будет придаваться специальное значение.— Прим. перев.
1 Принцип этот часто называют также принципом свертывания; в формулировке его обычно говорят не о форме, a d формуле, но мы (см. предыдущее примечание) предпочитаем резервировать этот термин для обозначения формальных выражений определенного вида (см. §§ 2.3, 2.7 и особенно 3.8).— Прим. перев
1 Разумеется, речь идет о сенате США — Прим. перев. и ред
[1] Здесь мы пользуемся обозначением, подробно обсуждаемым ниже.
1 См. §§ 2.1 и 2.2. —Прим.. пгрев.
1 Читатель, возможно, привык к использованию различных терминов для наименования какой-либо операции и ее результата: «умножение» — «произведение», «сложение»—«сумма», «вычитание» — «разность». В этой книге во многих случаях (хотя и не всегда) для обоих понятий используется один термин; к двусмысленностям это не приводит, поскольку из контекста ясно, о чем именно идет речь.— Прим. перев.
2 Под «рассуждением» здесь может пониматься и целая книга или даже некоторая научная теория; ср. ниже авторские примеры. Вместо «универсальное множество» часто говорят «универсум рассуждения» или просто «универсум».— Прим. перев.
3 Этот способ изображения отношений между множествами (или классами, понятиями, свойствами) известен также под именем «кругов Эйлера».— Прим. перев