
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Примеры решения некоторых типов задач
|
|
Примеры решения некоторых типов задач
Теория вероятностей
Задача 1.
Три стрелка стреляют в цель независимо друг от друга. Первый стрелок попадает в цель с вероятностью 0, 6, второй – с вероятностью 0, 7, а третий – с вероятностью 0, 75. Найти вероятность 1) хотя бы одного попадания в цель, если каждый стрелок сделает по одному выстрелу; 2) Первый и второй попадут в цель, а третий промахнется; 3) Трое стреляют, один промахнется; 4) Стреляют двое: первый и второй. Хотя бы один попадет.
Решение.
Событие Аi – «i – й стрелок попал в цель», противоположное событие 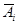 – «i – й стрелок не попал в цель», i = 1, 2, 3. Вероятности этих событий
– «i – й стрелок не попал в цель», i = 1, 2, 3. Вероятности этих событий
Р (А 1) = 0, 6, Р (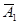 ) = 1 - Р (А 1) = 1 - 0, 6 = 0, 4;
) = 1 - Р (А 1) = 1 - 0, 6 = 0, 4;
Р (А 2) = 0, 7, Р (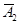 ) = 1 - Р (А 2) = 1 - 0, 7 = 0, 3;
) = 1 - Р (А 2) = 1 - 0, 7 = 0, 3;
Р (А 3) = 0, 75, Р (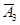 ) = 1 - Р (А 3) = 1 - 0, 75 = 0, 25.
) = 1 - Р (А 3) = 1 - 0, 75 = 0, 25.
1) Событие А - «хотя бы один стрелок попал в цель», противоположное событие 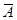 – «ни один стрелок не попал в цель».
– «ни один стрелок не попал в цель».
Событие 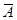 можно записать так
можно записать так 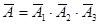 . Результаты выстрела любого из стрелков не зависят от результатов выстрелов других стрелков. Поэтому вероятность события
. Результаты выстрела любого из стрелков не зависят от результатов выстрелов других стрелков. Поэтому вероятность события 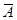 равна Р (
равна Р (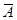 ) = Р (
) = Р ( ) =
) = 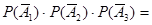 0, 4 ∙ 0, 3 ∙ 0, 25 = 0, 03.
0, 4 ∙ 0, 3 ∙ 0, 25 = 0, 03.
Искомая вероятность события А равна Р (А) = 1 - Р (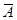 ) = 1 - 0, 03 = 0, 97.
) = 1 - 0, 03 = 0, 97.
2) Событие А - «Первый и второй попадут в цель, а третий промахнется», можно записать так 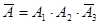 . Результаты выстрела любого из стрелков не зависят от результатов выстрелов других стрелков. Поэтому вероятность события
. Результаты выстрела любого из стрелков не зависят от результатов выстрелов других стрелков. Поэтому вероятность события 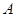 равна Р (
равна Р (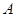 ) = Р (
) = Р (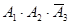 ) =
) = 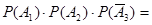 0, 6 ∙ 0, 7 ∙ 0, 25 = 0, 105.
0, 6 ∙ 0, 7 ∙ 0, 25 = 0, 105.
3) Событие В – «Трое стреляют, один промахнется», представляет собой совокупность (сумму) трех вариантов событий В = В1 + В2 + В3, где 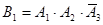 ,
, 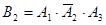 ,
, 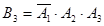 . Эти события не зависят друг от друга. Поэтому вероятность события В равна Р (В1+В2+В3) = Р (В1) + Р (В2) + Р (В3) = 0, 6 ∙ 0, 7 ∙ 0, 25 + 0, 6 ∙ 0, 3 ∙ 0, 75 + 0, 4 ∙ 0, 7 ∙ 0, 75 = 0, 105 + 0, 135 + 0, 21 = 0, 45.
. Эти события не зависят друг от друга. Поэтому вероятность события В равна Р (В1+В2+В3) = Р (В1) + Р (В2) + Р (В3) = 0, 6 ∙ 0, 7 ∙ 0, 25 + 0, 6 ∙ 0, 3 ∙ 0, 75 + 0, 4 ∙ 0, 7 ∙ 0, 75 = 0, 105 + 0, 135 + 0, 21 = 0, 45.
4) Стреляют двое: первый и второй. Событие А – «Хотя бы один попадет» является суммой совместных событий А = А1 + А2. Тогда искомая вероятность Р(А1+А2) = Р (А1) + Р (А2) – Р (А1 ∙ А2) = 0, 6 + 0, 7 – 0, 6 ∙ 0, 7 = 0, 88.
Ответ: 1) Вероятность хотя бы одного попадания в цель равна 0, 97. 2) Вероятность того, что первый и второй попадут в цель, а третий промахнется, равна 0, 105. 3) Вероятность того, что трое стреляют, один промахнется, равна 0, 453. 4) Вероятность того, что стреляют двое: первый и второй, и хотя бы один попадет, равна 0, 88.