
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 2. По данным задачи 1, используя критерий c2 - Пирсона, при уровне значимости α = 0,05 проверить гипотезу о том
|
|
По данным задачи 1, используя критерий c2 - Пирсона, при уровне значимости α = 0, 05 проверить гипотезу о том, что случайная величина Х – сумма вклада – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
2. Решение.
Проверяется гипотеза Н0: случайная величина Х – сумма вклада – распределена по нормальному закону. Функция плотности вероятности и функция распределения имеют вид
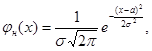
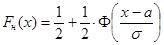 , где а, s - параметры распределения.
, где а, s - параметры распределения.
В качестве оценок этих параметров возьмем выборочное среднее значение и дисперсию.
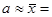 282; s =
282; s = 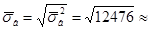 111, 696.
111, 696.
Тогда 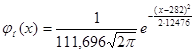 и
и 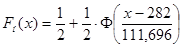 .
.
Вычислим наблюдаемое значение критерия Пирсона по формуле
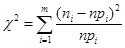 , где
, где
m - число интервалов; ni - частота (эмпирическая); n - объем выборки; pi - теоретическая
вероятность попадания случайной величины в i -ый интервал; npi - теоретическая частота.
Вероятность pi попадания случайной величины Х в интервал (xi; xi +1) найдем по формуле
pi = P (xi < X < xi +1) =
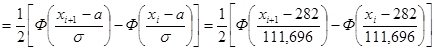 .
.
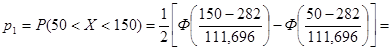
= 0, 5 × (Ф(-1, 18) - Ф(-2, 08)) = 0, 5 × (-0, 7620 + 0, 9625) = 0, 1002.
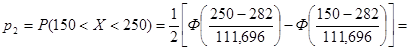
= 0, 5 × (Ф(-0, 29) - Ф(-1, 18)) = 0, 5 × (-0, 2282 + 0, 7620) = 0, 2669.
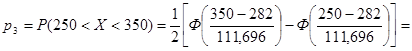
= 0, 5 × (Ф(0, 61) - Ф(-0, 29)) = 0, 5 × (0, 4581 + 0, 2282) = 0, 3432.
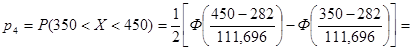
= 0, 5 × (Ф(1, 50) - Ф(0, 61)) = 0, 5 × (0, 8664 - 0, 4581) = 0, 2041.
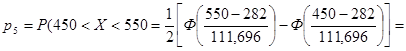
= 0, 5 × (Ф(2, 40) - Ф(1, 50)) = 0, 5 × (0, 9836 - 0, 8664) = 0, 0586.
Для расчета составим вспомогательную таблицу
| i | Интервал (xi; xi+1) | Эмпирические частоты ni | Вероятность pi | Теоретические частоты npi | ni - npi | (ni - npi)2 | (ni - npi)2 / npi |
| 50 - 150 | 0, 1002 | 10, 020 | 3, 980 | 15, 8404 | 1, 5809 | ||
| 150 - 250 | 0, 2669 | 26, 690 | -2, 690 | 7, 2361 | 0, 2711 | ||
| 250 - 350 | 0, 3432 | 34, 320 | 0, 680 | 0, 4624 | 0, 0135 | ||
| 350 - 450 | 0, 2041 | 20, 410 | -0, 410 | 0, 1681 | 0, 0082 | ||
| 450 - 550 | 0, 0586 | 5, 860 | 1, 140 | 1, 2996 | 0, 2218 | ||
| Суммы | 0, 9730 | 97, 300 | 2, 0955 |
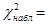 2, 0955.
2, 0955.
Найдем по таблице критическое значение критерия 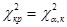 , k = m – s – 1, m = 5 - число интервалов, s = 2 - число параметров распределения, a = 0, 05 - уровень значимости, k = 5 - 2 - 1 = 2,
, k = m – s – 1, m = 5 - число интервалов, s = 2 - число параметров распределения, a = 0, 05 - уровень значимости, k = 5 - 2 - 1 = 2, 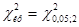 = 5, 99.
= 5, 99.
Сравниваем наблюдаемое значение критерия с критическим 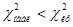
2, 0955 < 5, 99. Это означает, что наблюдаемое значение не попало в критическую область. Поэтому гипотеза о нормальном распределении размера кредита согласуется с данными выборки и должна быть принята.
Гистограмма - это совокупность прямоугольников, основаниями которых служат частичные интервалы (xi; xi +1], а высота которых равна 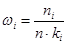 .
.
ki = xi +1 - xi - длина частичного интервала, ki = 100, n × ki = 100 × 100 = 10000
 ,
, 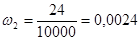 ,
, 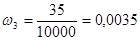 ,
, 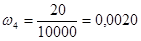 ,
,
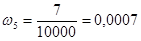 .
.
Для построения графика нормальной кривой отметим точки (xi; pi / k), где xi - середина интервала, pi - вероятность попадания в интервал.
Вершина при х = а = 282.
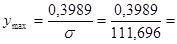 0, 0574.
0, 0574.
p1 / k = 0, 1002 / 100 = 0, 0010 p2 / k = 0, 2669 / 100 = 0, 0027
p3 / k = 0, 3432 / 100 = 0, 0034 p4 / k = 0, 2041 / 100 = 0, 0020
p5 / k = 0, 0586 / 100 = 0, 0006
 |