Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 3. 3. Распределение 250 пар, вступивших в брак, по возрасту мужчин Х (лет) и женщин Y (лет) представлено в таблице:
|
|
3. Распределение 250 пар, вступивших в брак, по возрасту мужчин Х (лет) и женщин Y (лет) представлено в таблице:
| y x | 15 - 25 | 25 - 35 | 35 - 45 | 45 - 55 | 55 - 65 | Итого: |
| 15 - 25 | ||||||
| 25 - 35 | ||||||
| 35 - 45 | ||||||
| 45 - 55 | ||||||
| 55 - 65 | ||||||
| 65 - 75 | ||||||
| Итого: |
Необходимо:
1) Вычислить групповые средние 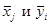 , построить эмпирические линии регрессии.
, построить эмпирические линии регрессии.
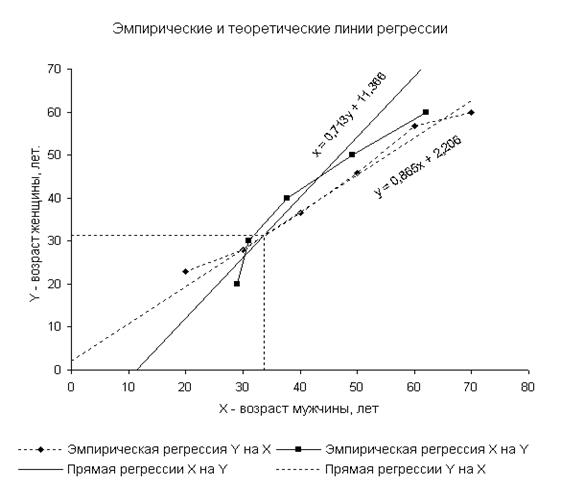
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать содержательную интерпретацию полученных уравнений; б) вычислить коэффициент корреляции на уровне значимости α = 0, 05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y; в) используя соответствующее уравнение регрессии, оценить средний возраст мужчин, имеющих супруг в возрасте 30 лет.
3. Решение.
По исходным данным составим корреляционную таблицу, где интервалы представлены своими серединами.
| yj xi | ni | |||||
| nj |
1) Найдем групповые средние по Y по формуле 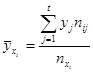 .
.
x1 = 20 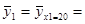 (20 × 7 + 30 × 3) / 10 = 230 / 10 = 23, 000
(20 × 7 + 30 × 3) / 10 = 230 / 10 = 23, 000
x2 = 30 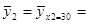 (20 × 52 + 30 × 110 + 40 × 13 + 50 × 1) / 176 = 4910 / 176 = 27, 898
(20 × 52 + 30 × 110 + 40 × 13 + 50 × 1) / 176 = 4910 / 176 = 27, 898
x3 = 40 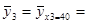 (20 × 1 + 30 × 14 + 40 × 23 + 50 × 2) / 40 = 1460 / 40 = 36, 500
(20 × 1 + 30 × 14 + 40 × 23 + 50 × 2) / 40 = 1460 / 40 = 36, 500
x4 = 50 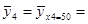 (30 × 1 + 40 × 4 + 50 × 6 + 60 × 1) / 12 = 550 / 12 = 45, 833
(30 × 1 + 40 × 4 + 50 × 6 + 60 × 1) / 12 = 550 / 12 = 45, 833
x5 = 60 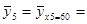 (50 × 3 + 60 × 6) / 9 = 510 / 9 = 56, 667
(50 × 3 + 60 × 6) / 9 = 510 / 9 = 56, 667
x6 = 70 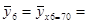 60 × 3 / 3 = 60, 000
60 × 3 / 3 = 60, 000
Составим таблицу 2.
| Таблица 2 | ||||||
| xi | ||||||
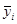
| 23, 000 | 27, 898 | 36, 500 | 45, 833 | 56, 667 | 60, 000 |
По точкам (хi; 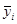 ) построим эмпирическую линию регрессии Y на X. Эти точки расположены вблизи прямой с уравнением y = ax + b, где a и b неизвестные параметры и их нужно определить.
) построим эмпирическую линию регрессии Y на X. Эти точки расположены вблизи прямой с уравнением y = ax + b, где a и b неизвестные параметры и их нужно определить.
Групповые средние по Х найдем по формуле 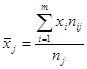 .
.
y1 = 20 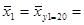 (20 × 7 + 30 × 52 + 40 × 1) / 60 = 1740 / 60 = 29, 000
(20 × 7 + 30 × 52 + 40 × 1) / 60 = 1740 / 60 = 29, 000
y2 = 30 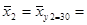 (20 × 3 + 30 × 110 + 40 × 14 + 50 × 1) / 128 = 3970 / 128 = 31, 016
(20 × 3 + 30 × 110 + 40 × 14 + 50 × 1) / 128 = 3970 / 128 = 31, 016
y3 = 40 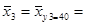 (30 × 13 + 40 × 23 + 50 × 4) / 40 = 1510 / 40 = 37, 750
(30 × 13 + 40 × 23 + 50 × 4) / 40 = 1510 / 40 = 37, 750
y4 = 50 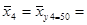 (30 × 1 + 40 × 2 + 50 × 6 + 60 × 3) / 12 = 590 / 12 = 49, 167
(30 × 1 + 40 × 2 + 50 × 6 + 60 × 3) / 12 = 590 / 12 = 49, 167
y5 = 60 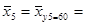 (50 × 1 + 60 × 6 + 70 × 3) / 10 = 620 / 10 = 62, 000
(50 × 1 + 60 × 6 + 70 × 3) / 10 = 620 / 10 = 62, 000
Составим таблицу 3
| Таблица 3 | |||||
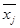
| 29, 000 | 31, 016 | 37, 750 | 49, 167 | 62, 000 |
| yj |
По точкам (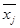 ; yj) построим эмпирическую линию регрессии X на Y. Эти точки расположены вблизи прямой с уравнением x = cy + d, где c и d неизвестные параметры и их нужно определить.
; yj) построим эмпирическую линию регрессии X на Y. Эти точки расположены вблизи прямой с уравнением x = cy + d, где c и d неизвестные параметры и их нужно определить.
Для получения уравнений прямых регрессий вычислим выборочные средние
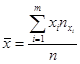 и
и 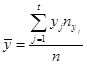 .
.
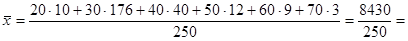 33, 72
33, 72
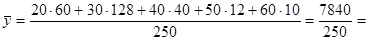 31, 36
31, 36
Выборочные дисперсии находим по формулам 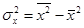 и
и 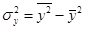
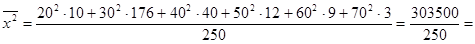 1214
1214
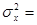 1214 – 33, 722 = 76, 9616.
1214 – 33, 722 = 76, 9616.
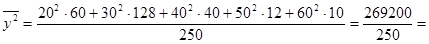 1076, 8
1076, 8
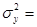 1076, 8 – 31, 362 = 93, 3504.
1076, 8 – 31, 362 = 93, 3504.
Вычислим средние квадратические отклонения
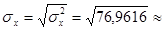 8, 7728;
8, 7728;  9, 6618.
9, 6618.
Вычислим 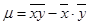 по формуле
по формуле 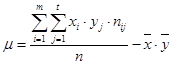 .
.
m = (20 × 20 × 7 + 20 × 30 × 3 + 30 × 20 × 52 + 30 × 30 × 110 + 30 × 40 × 13 + 30 × 50 × 1 +
+ 40 × 20 × 1 + 40 × 30 × 14 + 40 × 40 × 23 + 40 × 50 × 2 + 50 × 30 × 1 + 50 × 40 × 4 +
+ 50 × 50 × 6 + 50 × 60 × 1 + 60 × 50 × 3 + 60 × 60 × 6 + 70 × 60 × 3) / 250 – 33, 72 × 31, 36 =
= 281000 / 250 – 1057, 4592 = 1124 – 1057, 4592 = 66, 5408.
Вычислим коэффициенты регрессии по формулам
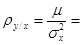 66, 5408: 76, 9616» 0, 8646» 0, 865;
66, 5408: 76, 9616» 0, 8646» 0, 865;
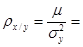 66, 5408: 93, 3504» 0, 7128» 0, 713.
66, 5408: 93, 3504» 0, 7128» 0, 713.
а) Составим уравнение регрессии X на Y 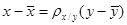
x – 33, 72 = 0, 713 × (y – 31, 36) или x = 0, 713 y + 11, 366.
Прямую проведем через точки (33, 72; 31, 36) и (11, 366; 0, 00).
Уравнение регрессии X на Y показывает средний возраст мужчины, вступившего в брак с женщиной возраста y.
Содержательный смысл коэффициента регрессии 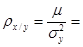 0, 713 состоит в том, что при увеличении возраста женщины, вступающей в брак, на 1 год возраст супруга увеличивается в среднем на 0, 713 года.
0, 713 состоит в том, что при увеличении возраста женщины, вступающей в брак, на 1 год возраст супруга увеличивается в среднем на 0, 713 года.
Составим уравнение регрессии Y на X 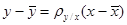
y – 31, 36 = 0, 865 × (x – 33, 36) или y = 0, 865 x + 2, 206.
Прямую проведем через точки (33, 72; 31, 36) и (0, 00; 2, 206).
Уравнение регрессии Y на X показывает средний возраст женщины, вступившей в брак с мужчиной возраста х.
Содержательный смысл коэффициента регрессии 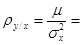 0, 865 состоит в том, что при увеличении возраста мужчины, вступающего в брак, на 1 год возраст супруги увеличивается в среднем на 0, 865 года.
0, 865 состоит в том, что при увеличении возраста мужчины, вступающего в брак, на 1 год возраст супруги увеличивается в среднем на 0, 865 года.
б) Коэффициент корреляции 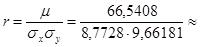 0, 7850.
0, 7850.
Для проверки значимости коэффициента корреляции вычислим наблюдаемое значение
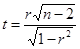 ;
; 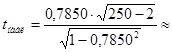 19, 958.
19, 958.
Критическое значение для уровня значимости α = 0, 05 и числа степеней свободы k = n–2= = 250 -2 = 248 находим по таблице t1- 0, 05; 248 = t0, 95; 248 = 1, 97.
Получили |tнабл| > tкр, так как 19, 958 > 1, 97.
Следовательно, коэффициент корреляции значимо отличается от нуля.
Коэффициент корреляции r = 0, 7851 > 0 и попадает по абсолютной величине в интервал 0, 7 - 0, 99. Следовательно, между возрастом вступающих в брак мужчины (Х) и женщины (Y) существует прямая сильная корреляционная связь. При увеличении (уменьшении) значения одной величины соответственно увеличивается (уменьшается) среднее значение другой.
в) Используем уравнение прямой регрессии Х на Y x = 0, 713 y + 11, 366.
При y = 30 х = 0, 713 × 30 + 11, 366 = 32, 756.
Средний возраст мужчин, имеющих супруг в возрасте 30 лет, равен 32, 756 лет.