Решение. Событие А – «студент сдаст экзамен по математике на «отлично»» – происходит с вероятностью р = Р(А) = 0,05; q = 1 - р = 1- 0,05 = 0,95

Событие А – «студент сдаст экзамен по математике на «отлично»» – происходит с вероятностью р = Р (А) = 0, 05; q = 1 - р = 1- 0, 05 = 0, 95. Число испытаний n = 100.

Так как вероятность р события А мала, число испытаний n достаточно велико и

np = 100 ∙ 0, 05 = 5 < 10, то можно применить асимптотическую формулу Пуассона:

,

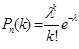где l = np = 5; e ^{- l} = e ^-5» 0, 00674.

а) Событие В – «из 100 наудачу выбранных студентов сдадут экзамен по математике на «отлично» два студента». Его вероятность

Р (В) = Р ₁₀₀(2) = 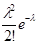= 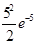» 12, 5´ 0, 00674» 0, 0842.

б) Событие С – «из 100 студентов сдадут экзамен по математике на «отлично» не менее пяти студентов». Его вероятность равна

Р (С) = Р ₁₀₀(k ³ 5) = 1 – Р ₁₀₀(k £ 4) = 1 – (Р ₁₀₀(0) + Р ₁₀₀(1) + Р ₁₀₀(2) + Р ₁₀₀(3) + Р ₁₀₀(4)).

Р (С)» 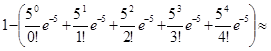1 – e ^-5 ´ (1 + 5 + 12, 5 + 20, 8333 + 26, 0417)»

» 1 – 0, 00674´ 65, 375» 0, 5594.

Ответ:

а) вероятность того, что из 100 наудачу выбранных студентов сдадут экзамен по математике на «отлично» два студента, приближенно равна 0, 0842;

б) вероятность того, что из 100 студентов сдадут экзамен по математике на «отлично» не менее пяти студентов, приближенно равна 0, 5594.