Задача 1. С целью определения средней суммы вкладов в сберегательном банке, имеющем 2000 вкладчиков, по схеме собственно-случайной бесповторной выборки проведено

С целью определения средней суммы вкладов в сберегательном банке, имеющем 2000 вкладчиков, по схеме собственно-случайной бесповторной выборки проведено обследование 100 вкладов. Результаты обследования представлены в таблице:

Найти: а) границы, в которых с вероятностью 0, 9488 находится средняя сумма всех вкладов в сберегательном банке; б) объем бесповторной выборки, при котором те же границы для средней суммы вкладов в сберегательном банке (см. п. а)) можно гарантировать с вероятностью 0, 9; в) вероятность того, что доля всех вкладчиков, у которых сумма вклада больше 250 тыс. руб., отличается от доли таких вкладчиков в выборке не более чем на 0, 1 (по абсолютной величине).

1. Решение.

От интервального распределения перейдем к дискретному, взяв в качестве представителя интервала его середину .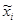

Для расчета выборочной средней и выборочной дисперсии составим таблицу.

Сумма вклада, тыс. руб.	Количество вкладов, ni	Середина, хi	хi - C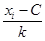
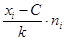
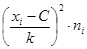
50 - 150			-200	-2	-28
150 - 250			-100	-1	-24
250 - 350
350 - 450
450 - 550
Суммы					-18

С = 300 - середина интервала с наибольшей частотой;

k = 100 - величина интервала.

Выборочное среднее найдем по формуле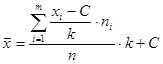

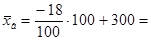282 тыс. руб.

Выборочная дисперсия

,

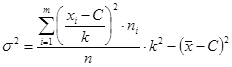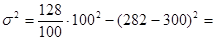12476.

Выборочное среднее квадратическое отклонение

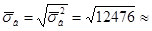111, 696.

а) Средняя квадратическая ошибка среднего значения признака для бесповторной выборки .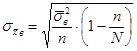

Число всех вкладов N = 2000, объем выборки n = 100

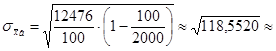10, 8868.

Вероятности β = 0, 9488 соответствует t = 1, 95, так как Ф(1, 95) = 0, 9488.

Предельная ошибка 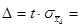1, 95 × 10, 8868» 21, 2270.

Нижняя граница 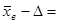282 - 21, 227 = 260, 773,

верхняя граница 282 + 21, 227 = 303, 227.

С вероятностью 0, 9488 средняя сумма всех вкладов в сберегательном банке заключена в границах от 260, 773 до 303, 227 тыс. руб.

б) Вероятности Р = 0, 9 соответствует t = 1, 64, так как Ф(1, 64) = 0, 9.

Число вкладчиков, которых надо обследовать для повторной выборки

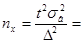
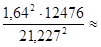74, 912.

Для бесповторной выборки

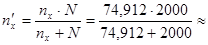72, 207. Округляем до большего целого 73.

Чтобы с вероятностью 0, 9 гарантировать те же границы для средней суммы всех вкладов в сберегательном банке, что и в п. а) объем бесповторной выборки должен быть равным 73 вкладам.

в) Выборочная доля вкладчиков, у которых сумма вклада больше 250 тыс. руб., равна 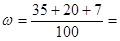0, 62.

Средняя квадратическая ошибка доли для бесповторной выборки

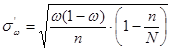
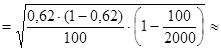
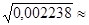0, 0473» 0, 047.

Предельная ошибка Δ = 0, 1. 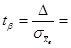0, 1 / 0, 0473» 2, 11.

Находим требуемую вероятность P = Ф(t_β ) = Ф(2, 11) = 0, 9651

Вероятность того, что доля всех вкладчиков, у которых сумма вклада больше 250 тыс. руб., отличается от доли таких вкладчиков в выборке не более чем на 0, 1(по абсолютной величине), приближенно равна 0, 9651.