
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общая теория кривых второго порядка
|
|
Удобно будет рассматривать уравнение кривой второго порядка
в следующем виде:
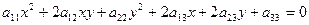 (1)
(1)
Сформулируем признаки, позволяющие узнать тип линии по ее уравнению (1).
Введем некоторые определения.
Группу слагаемых a11x2+2а21xy+а22у2 назовем группой старших членов. Группу слагаемых 2а13х+2а23у+а33 назовем линейной частью уравнения (1).
Коэффициенты а11, a12, а22 назовем коэффициентами группы старших членов или старшими коэффициентами, а коэффициенты а13, а23, а33 — коэффициентами линейной части или линейными коэффициентами. Отметим, что коэффициент а33 также называется свободным членом уравнения (1).
Осуществим параллельный перенос системы координат ОХY вточку 0'(х0, у0), Тогда, как известно, х=х'+х0, у=у'+у0 и в новой системе координат уравнение (1) примет вид:
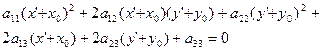
Обозначим коэффициенты при степенях неизвестных в уравнении (*) следующим образом:
Пусть дан определитель
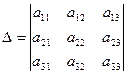
Тогда минором элемента aij определителя Δ называется определитель Mij полученный из данного, вычеркиванием строки и столбца, на пересечении которых стоит элемент аij.
Имеет место следующее равенство:
Δ =(-1)i+1ai1Mi1+(-1)i+2ai2Mi2+(-1)i+3ai3Mi3 (*)
(разложение по элементам i-й строки.) Доказательство. Если i=2, то поменяем местами 2-ю и 1-ю строки. Получаем определитель Δ 1, равный —Δ (свойство 2).
Если i=3, то поменяем вначале 3-ю строку со 2-й, а затем
полученную вторую с первой. Получим определитель Δ 2, равный
Δ (свойство 2). Итак,
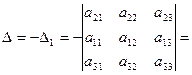
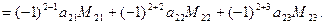
Аналогично,
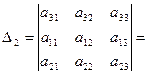
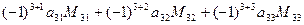 .
.
В дальнейшем, под системой координат будем понимать прямоугольную систему координат.