
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение прямой в пространстве
|
|
Очевидно, что прямую в пространстве можно задать как линию пересечения двух плоскостей α 1 и α 2. Тогда в произвольной афинной системе координат прямая задается системой двух линейных уравнений
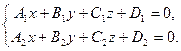 (1)
(1)
- общее уравнение прямой или уравнение прямой в общем виде.
Классификация кривых второго порядка (КВП)
Уравнение вида
a x2+ b ху+ с у2+ d x+ е у+ f =0, (1)
где a² + b² + c² ≠ 0, называется уравнением кривой второго порядка в прямоугольноу системе ккординат OXY. Преобразуем систему координат таким образом, чтобы уравнение (1) приняло наиболее простой вид.
1. Если в уравнении коэффициент b ≠ 0, то можно повернуть систему координат OXY на угол α такой, что в новой системе координат O’X’Y’ уравнение (1) не будет содержать член с произведением x’y’.
Действительно, согласно формулам поворота x = x’cosα – y’sinα, y = y’sinα + y’cosα.. Подставляя значения x и y в (1) легко подсчитать, что коэффициент при x’y’ примет вид
-2 a cosα sinα + b ² cos² α - b ² sin² α + 2 c sinα cosα.
Упрощая, получаем
- a sin2α + b cos2α + c sin2α = 0,
(a - c)sin2α = b cos2α, т.е.
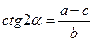 ,
,
Таким образом, в дальнейшем предполагаем, что уравнение КВП имеет вид
a x2+ b ху+ с у2+ d x+ е у+ f =0. (2)
2. Если в уравнении (2) а ≠ 0 и d ≠ 0, либо с ≠ 0 и е ≠ 0, то, осуществляя параллельный перенос системы координат ОХУ, получаем уравнение КВП, не содержащее член с х, соответственено у.
Действительно, пусть а ≠ 0, d ≠ 0. Выделим полный квадрат при переменной х в (2).