Фокальный параметр эллипса и гиперболы

Пусть эллипс и гипербола заданы соответственно своими каноническими уравнениями. Проведем через один из фокусов этих кривых прямую перпендикулярную оси ОХ и обозначим точки ее пересечения с кривой через Р и Р'.

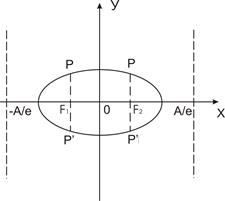
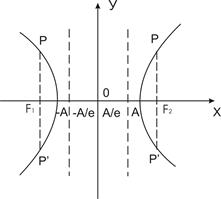
Обозначим длину отрезка РР' через 2р. Тогда величина р(р> 0) называется фокальным параметром эллипса (гиперболы) и равна: .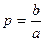

Если обозначить через d – расстояние между фокусом и деректрисой, то .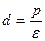

Так как для параболы ε = 1 и d = р, то делаем следующий Вывод: для эллипса (кроме окружности), гиперболы, парабол фокальный параметр р равен:

p = ε d,

где c – эксцентриситет, d – расстояние от фокуса до соответствующей директрисы.

Заметим, что для окружности фокальный параметр равен ее радиусу.

Определение. Эксцентриситетом гиперболы называется величина

.

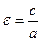Так как для гиперболы с > а, и следовательно, чем меньше ε, тем более сжата гипербола к оси ОХ.