Полярное уравнение эллипса, гиперболы, параболы

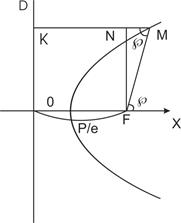
Выведем полярное уравнение для отличного от окружности эллипса, параболы или правой ветви гиперболы. Для этого совместим полюс полярной системы координат с левым фокусом эллипса (правым фокусом гиперболы) или единственным фокусом параболы, а полярную ось направим перпендикулярно директрисе d, соответствующей фокусу. Обозначим через F, р и ε соответственно фокус, фокальный параметр и эксцентриситет кривой. Пусть М — произвольная точка кривой, МF = r — полярный радиус точки М, φ — ее полярный угол. Тогда

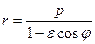
- полярное уравнение эллипса, отличного от окружности, параболы, правой ветви гиперболы.

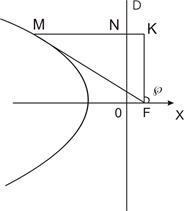
Для левой ветви гиперболы

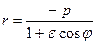
- полярное уравнение левой ветви гиперболы.

Пусть l – прямая. Тогда ее положение в пространстве однозначно определяется заданием ее направляющего вектора =(m, n, р) и точкой М₀(х ₀, у ₀, z ₀), через которую прямая проходит. Возьмем произвольную точку М(х, у, z) 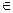l. Тогда 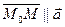и, значит,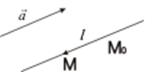

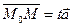
Переходя к координатам, получим

x - x ₀ = tm, y - y ₀ = tn, z - z ₀ = tp

- параметрические уравнение прямой.

Выражая параметр t, получим

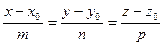
- каноническое уравнение прямой, проходящей через точку М₀(х₀ y₀, z₀) параллельно вектору =(m, m, р).

Последнее уравнение равносильно

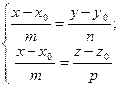
- общее уравнение прямой.

Пусть M₁{ x ₁, у ₁, z ₁) и М₂(х ₂, у ₂, z ₂) – точки прямой. Тогда

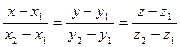
- уравнение прямой, проходящей через две заданные точки.

Наоборот, пусть задано общее уравнение прямой.

Беря произвольную точку М₀(х₀, у₀, z₀) прямой получаем

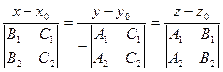
- каноническое уравнение прямой.