Взаимное расположение прямой и плоскости

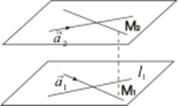
Пусть прямая l и плоскость α заданы соответственно уравнениями

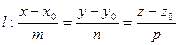, α: A x + B y + C z + D = 0.

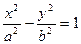. (3)

По свойствам уравнения (3) исследуем свойства гиперболы:

1. Координатные оси являются осми симметрии гиперболы. Поэтому гиперболу достаточно исследовать только в первой координатной четверти.

2. Если у = 0, то x = 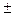а. Если х = 0, то уравнение (3)

решений не имеет. Значит, гипербола пересекает только ось ОХ в точках А₁(— а, 0), А₂(а, 0), называемых вершинами гиперболы.

3. Так как

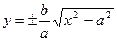|х| 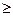а. Поэтому гипербола расположена вне полосы, ограниченной прямыми x= 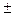а.

4. Если x возрастает от а до + 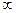, то из (1.12) следует, что у возрастает от 0 до + 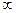в первой координатной четверти.

5.

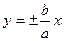
- наклонные асимптоты гиперболы.

По полученным свойствам строим гиперболу (рис.7). Отрезок А₁А₂ и его длина 2 а называются действительной осью гиперболы, а отрезок ОА₁ и его длина а — действительной полуосью. Отрезок В₁В₂ и его длина 2 b — мнимая ось гиперболы, а отрезок ОВ₁ и его длина b — мнимая полуось. Длина отрезка F₁F₂=2 с называется фокусным расстоянием, начало координат — центр гиперболы.

x ²— у ²= а ²

Определение. Эксцентриситетом эллипса называется число

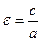
Так как с< а, то 0< c < 1. Заметим, что у окружности оба фокуса

совпадают, поэтому с = 0 и ε = 0.

.

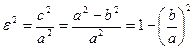Следовательно, эксцентриситет характеризует форму эллипса.

Используя понятия эксцентриситета, можно выразить фокальные радиусы произвольной точки M(x, у) эллипса:

r₁= а +ε х, r₂= а —ε х