
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общее уравнение прямой. Уравнение прямой в отрезках.
|
|
Пусть задана некоторая афинная система координат OXY.
Теорема 2.1. Любая прямая l системе координат ОX задается линейным уравнением вида
А x + B y + С = О, (1)
где А, В, С 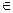 R и А2 + В2
R и А2 + В2  0. Обратно, любое уравнение вида (1) задает прямую.
0. Обратно, любое уравнение вида (1) задает прямую.
Уравнение вида (1) - общее уравнение прямой.
Пусть в уравнении (1) все коэффициенты А, В и С отличны от нуля. Тогда
-Ах-By=-С, и 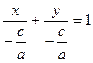 .
.
Обозначим -С/А=а, -С/B=b. Получим
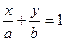
- уравнение в отрезках.
Действительно, числа |а| и |b| указывают на величины отрезков, отсекаемых прямой l на осях ОХ и OY соответственно.
Пусть прямая l задана общим уравнением (1) в прямоугольной системе координат и пусть точки M1(x1, у1) и М2(х2, у2) принадлежит l. Тогда
А x 1 + В у 1 + С = А х 2 + В у 2 + С, то есть A(x 1- x 2) + В(у 1- у 2) = 0.
Последнее равенство означает, что вектор 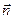 =(А, В) ортогонален вектору
=(А, В) ортогонален вектору 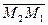 =(x1-x2, у1-у2). т.е.
=(x1-x2, у1-у2). т.е. 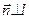 Вектор
Вектор 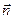 (А, В) называется нормальным вектором прямой l.
(А, В) называется нормальным вектором прямой l.
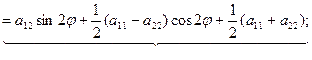
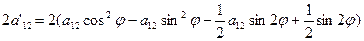 , т.е.
, т.е.
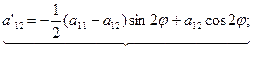
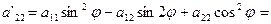
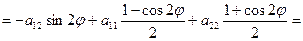

a'13=a13cosφ +a23cosφ
a'23=a23cosφ -a13sinφ
a'33=a33 (4)
Вывод: старшие коэффициенты а'11, а'12 и а'22, выражаются только через угол φ старшие коэффициенты а11, а12 и а22. Коэффициенты а'13 и а'23 выражаются только через угол φ и коэффициенты а13, а23. Коэффициенты а'33 и а33 равны.
Для упрощения равенств (4) введем следующие обозначения:

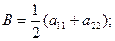
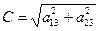 .
.
Тогда
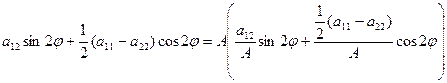 ,
,
если А  0. Введем угол α, где
0. Введем угол α, где
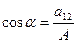 ,
, 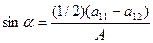
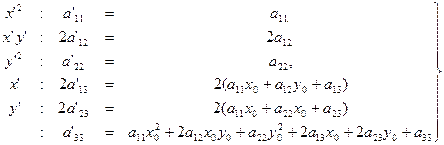 (2)
(2)
Тогда уравнение (*) примет вид:
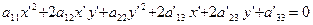 (3)
(3)
Вывод: при параллельном переносе системы координат, коэффициенты группы старших членов не изменяются, а коэффициенты линейной части изменяются по формулам (2).
Применим формулы поворота системы ОХУ на угол φ т.е.
х=х'соsφ -y'sinφ;
y=x'sinφ +y'cosφ;
Получим:
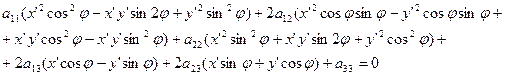
Тогда в новой системе координат, уравнение (1) примет вид:
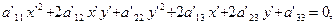
где
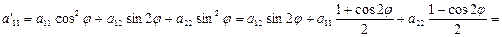
Рассмотрим вектор 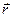 =(-В, А). Тогда
=(-В, А). Тогда
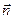
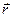 =А(-В)+ВА=0. т.е.
=А(-В)+ВА=0. т.е. 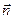 ^
^ 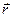 .
.
Следовательно, вектор 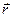 =(-В, А) является направляющим вектором пряной l.
=(-В, А) является направляющим вектором пряной l.