
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Координаты в пространстве.
|
|
Определение. Пусть в пространстве заданы три координатные оси OX, OY и OZ с некомпланарными ортами 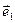 ,
, 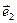 ,
, 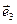 соответственно. Тогда четверка (0,
соответственно. Тогда четверка (0, 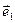 ,
, 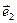 ,
, 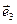 ) называется афинным репером, или афинной системой координат в пространстве.
) называется афинным репером, или афинной системой координат в пространстве.
Точка 0 - начало координат, векторы 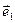 ,
, 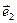 ,
, 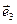 - базисные векторы.
- базисные векторы.
Так как векторы 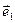 ,
, 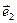 ,
, 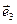 - линейно независимы, то для
- линейно независимы, то для
любого вектора 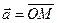 имеет место разложение:
имеет место разложение:
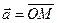 = x
= x 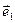 + y
+ y 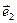 + z
+ z 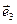
Числа x, y, z называются координатами точки М (записывается: М (х, у, z)), 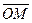 называется радиус-вектором точки М с координатами х, у, z (записывается: ОМ = (х, у, z)), причем х называется абсциссой, у - ординатой, z - аппликатой.
называется радиус-вектором точки М с координатами х, у, z (записывается: ОМ = (х, у, z)), причем х называется абсциссой, у - ординатой, z - аппликатой.
Афинную систему часто обозначают через OXYZ. Оси OX, OY, OZ называют соответственно осями абсцисс, ординат и аппликат. Плоскости, определяемые координатными осями, т.е. OXY, OYZ, OXZ, называют координатными плоскостями. Эти плоскости делят все пространство на восемь частей, называемых координатными ок-
Так как I2=a11a22—а122=О, то из (*) следует, что -(a112/2) -(а222/2)=а122.. Значит, a11=a22=a12=0 – противоречие с тем, что уравнение (1) — уравнение кривой второго порядка.
Заметим, что если в уравнении (1) а12  О, то путем поворота системы координат 0ХУ можно придти к уравнению вида (14)
О, то путем поворота системы координат 0ХУ можно придти к уравнению вида (14)
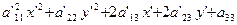
Так как I1=а'11+а22  О, I2=a'11а'22=О, то один из коэффициентов a'11 и а'22 равен нулю, а другой не равен нулю.
О, I2=a'11а'22=О, то один из коэффициентов a'11 и а'22 равен нулю, а другой не равен нулю.
Будем считать, что а'11=О, а'22  0 (случай а'11
0 (случай а'11  О, a'22=0
О, a'22=0
рассматривается аналогично). Тогда I1=a'22 и уравнение (14)
можно записать так:
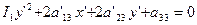 (25)
(25)
Осуществим теперь параллельный перенос:
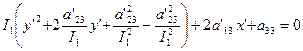 , т.е.
, т.е.
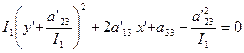 . (26)
. (26)
Тогда x" =x' и у" =у'+а'23/I1. Значит, в новой системе координат
О" Х" У" уравнение КВП примет вид:
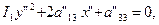 (27)
(27)
где 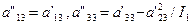
Теорема 1.5. Пусть уравнение (1) — есть уравнение параболического типа. Тогда при I3  0 это уравнение параболы, а при I3=0 — это уравнение либо пары параллельных действительных прямых, либо пары мнимых параллельных прямых.
0 это уравнение параболы, а при I3=0 — это уравнение либо пары параллельных действительных прямых, либо пары мнимых параллельных прямых.
то из I2< 0 следует а" 11, и а" 22 имеют разные знаки. Пусть а" 11> 0, а" 22< О, тогда уравнение (18) можно записать так:
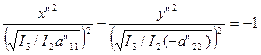 , при I3< 0; (22)
, при I3< 0; (22)
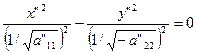 , при I3=0; (23)
, при I3=0; (23)
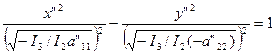 , при I3> 0; (24)
, при I3> 0; (24)
Уравнение (22) задает гиперболу, симметричную относительно
оси О" Y".
Уравнение (23) можно переписать так:
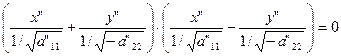
– пара пересекающихся прямых в системе координат 0" Х" Y".
Уравнение (24) — каноническое уравнение гиперболы.
Случай, когда а11" < О, а22" > 0 рассматривается аналогично.
Теорема доказана.