Конические поверхности

Определение. Конической поверхностью называется множество прямых (образующих), проходящих через некоторую точку (вершину) и пересекающих некоторую линию (направляющую).

Коническая ПВП — коническая поверхность с направляющей, являющейся КВП.

поверхности параллельны оси OZ, а направляющая лежит в плоскости OXY и задается уравнением:

F(x, у) =0

Если взять произвольную точку M(z, y, z) на цилиндрической поверхности, то ее проекция на плоскость OXY есть точка M₁(х₁, у₁, 0). Так как точки M и М₁ лежат на образующей, то х₁=х, у₁=у. А так как точка М₁ лежит на направляющей, то координаты точки М₁, а, значит, и точки M, удовлетворяют уравнению F(x, у)=0.

Итак, уравнению удовлетворяют координаты любой точки

цилиндрической поверхности. Следовательно, уравнение

F(x, у)=0

– искомое уравнение цилиндрической поверхности.

Если в прямоугольной системе координат OXYZ направляющая является кривой второго порядка, задаваемой каноническим уравнением вида F(x, у)=0, а образующие параллельны оси OZ, то цилиндрическими поверхностями второго порядка будут:

1) х²+y²=z² — прямой круговой цилиндр;

2) 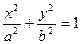- эллиптический цилиндр;

3) 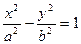- гиперболический цилиндр;

4) у²=2рх - параболический цилиндр.

3) ( + 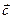) = + 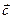(дистрибутивность).

Из определения следует, что

.

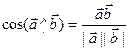Tеорема (необходимое и достаточное условие ортогональности двух векторов). Два ненулевых вектора взаимно перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю.