
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие вектора
|
|
Аналитическая геометрия.
Гомель, 2004
УДК 514 122
Рецензенты: Семенчук В.Н. – доктор физико-математических наук.
Скиба А.Н. – доктор физико-математических наук.
Дается краткое изложение курса лекций по аналитической геометрии для студентов, обучающихся по специальности «Прикладная математика»
Рекомендовано к печати ученым советом Гомельского государственного университета им. Ф. Скорины
© Гомельский государственный университет им. Ф. Скорины.
Учебное издание
ХОДАЛЕВИЧ АЛЕКСАНДР ДМИТРИЕВИЧ
Краткий курс лекций по геометрии и алгебре специальность
" Прикладная математика" " Аналитическая геометрия".
Подписано в печать __.__.__. Формат 60x84 1/16. Бумага писчая № 1
Печать офсетная. Усл. П. Л. 2, 3. Уч.-изд.л. 20. Тираж ___ экз.
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
Отпечатано на ризографе Учреждения образования
«Гомельский государственный университет имени
Франциска Скорины»
246019, г. Гомель, ул. Советская, 104
Литература:
1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М: Наука, 1979.
2. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976.
3. Бузланов А.В., Монахов В.С. Лабораторные работы по курсу «Алгебра и теория чисел». – Гомель: Ротапринт ГГУ им. Ф. Скорины, 1991.
4. Бузланов А.В., Каморников С.Ф., Кармазин А.П. Лабораторные работы по курсу «Алгебра и теория чисел» (раздел «Линейная алгебра») для студентов математического факультета. Часть I, II, III. – Гомель: Ротапринт ГГУ им. Ф. Скорины, 1990, 1991.
5. Бурдун А.А., Мурашко Е.А., Толкачёв М.М., Феденко А.О. Сборник задач по алгебре и аналитической геометрии. – Мн.: Университетское, 1989.
6. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1982.
7. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974.
8. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1968.
9. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Часть I, II. – Мн.: Вышэйшая школа, 1984, 1987.
10. Рублёв А.Н. Курс линейной алгебры и аналитической геометрии. – М.: Вышэйшая школа, 1972.
Аналитическая геометрия - это раздел математики, в котором геометрические объекты изучаются с помощью алгебраических методов, в основе которых лежит понятие координат.
ГЛАВА 1. ВЕКТОРЫ И КООРДИНАТЫ
Понятие вектора
Пусть А – произвольное непустое множество. Декартовым кваратом А называется множество
A 2 = 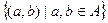
Бинарным отношением на А называется любое подмножество 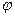 множества A 2.
множества A 2.
Отношением эквивалентности на А называется такое бинарное отношение 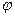 на А, которое удовлетворяет следующим условиям:
на А, которое удовлетворяет следующим условиям:
1) 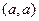
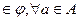 (рефлексивность);
(рефлексивность);
2) если (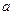 , b)
, b) 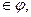 то (b,
то (b, 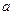 )
) 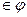 (симметричность);
(симметричность);
3) если (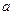 , b)
, b) 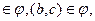 то (
то (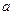 , c)
, c) 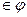 (транзитивность).
(транзитивность).
Теорема. Любое отношение эквивалентности на множестве А определяет разбиение этого множества на попарно непересекающиеся классы (классы эквивалентности). Обратно, любое разбиение множества А на попарно непересекающиеся классы определяет отношение эквивалентности на А.
Направленный отрезок – отрезок, у которого указано, какая точка является началом, а какая концом. Обозначается 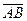 .
.
Пусть заданы направленные отрезки 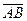 и
и 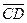 , не лежащие на двух различных параллельных прямых, и плоскость
, не лежащие на двух различных параллельных прямых, и плоскость  , проходящая через точки В и D. Тогда плоскость
, проходящая через точки В и D. Тогда плоскость  разбивает все пространство на два полупространства. Если при этом точки B и D лежат в одном полупространстве, то говорят, что направленные отрезки
разбивает все пространство на два полупространства. Если при этом точки B и D лежат в одном полупространстве, то говорят, что направленные отрезки 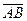 и
и 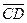 одинаково направлены (обозначается
одинаково направлены (обозначается 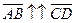 ). В противном случае,
). В противном случае,
они называются противоположно направленными (обозначается 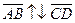 ).
).
Если направленные отрезки 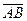 и
и 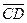 лежат на одной прямой, то они одинаково (противоположно) направленны, если существует такой третий направленный отрезок
лежат на одной прямой, то они одинаково (противоположно) направленны, если существует такой третий направленный отрезок 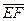 , который одинаково направлен с каждым из направленных отрезков
, который одинаково направлен с каждым из направленных отрезков 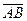 и
и 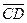 (противоположно направлен в точности с одним из направленных отрезков
(противоположно направлен в точности с одним из направленных отрезков 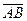 или
или 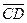 ).
).
Абсолютной величиной или модулем (длиной) направленного отрезка  называется длина этого направленного отрезка и обозначается |
называется длина этого направленного отрезка и обозначается |  |.
|.
Два направленных отрезка 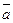 и
и 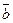 называются равными, если
называются равными, если 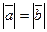 и
и 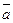
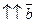 , при этом пишут
, при этом пишут 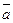 =
= 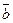 ,
,
Теорема. Отношение равенства направленных отрезков является отношением эквивалентности.
Тогда вектором называется абстрактный объект, совпадающий с некоторым классом эквивалентности.
Таким образом, каждый из равных друг другу направленных отрезков считается представлением (изображением) данного вектора, а неравные направленные отрезки считаются представлением разных векторов. Поэтому в дальнейшем вектор изображается точно так, как и соответствующий ему направленный отрезок.
Векторы 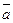 и
и 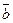 называются коллинеарными, если образующие их направленные отрезки параллельны одной и той же прямой (обозначается
называются коллинеарными, если образующие их направленные отрезки параллельны одной и той же прямой (обозначается 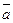 ||
|| 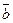 ).
).
Три и более векторов называются компланарными, если образующие их направленные отрезки параллельны некоторой плоскости.
Нулевым вектором называется вектор, начало которого совпадает с его концом (обозначается 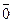 ). Направление нулевого вектора не определено.
). Направление нулевого вектора не определено.