Эллипсоид

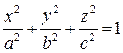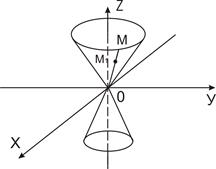
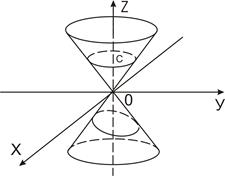
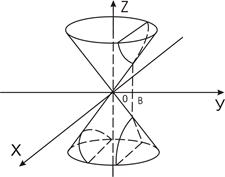
Если вершина совпадает с началом прямоугольной системы координат OXY, а направляющей служит эллипс:

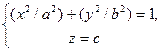
То уравнение конической поверхности имеет вид:

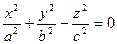
– уравнение конической поверхности

Пусть l - некоторая ось, α - плоскость, непараллельная оси l. Через произвольную точку А пространства проведем плоскость α '||α и обозначим точку пересечения плоскости α ' c осью l через А₁. Тогда точка А₁ называется проекцией точки А на ось l относительно плоскости α. В частности, если α 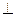l, то проекция называется прямоугольной, или ортогональной.

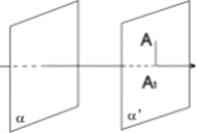
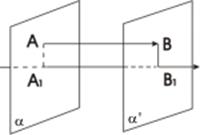
Пусть теперь задан вектор 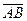. Возьмем проекции А₁ и В₁ точек А и В на ось l относительно плоскости α.

Тогда вектор 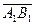называется проекциейвектора 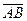на ось l относительно плоскости α. Величиной проекции вектора 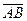на ось l относительно плоскости α называется число, равное:

а) | 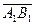|, если направление вектора 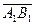совпадает с направлением оси l;

б) - | 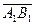|, если направление 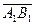противоположно направлено оси l.

Обычно из контекста ясно о проекции относительно какой плоскости идет речь. Поэтому величину проекции вектора 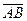на ось l будем обозначать Пр _l 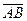, а для ортогональной проекции использовать обозначение Пр _l .

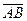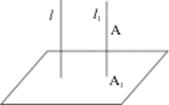Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l ₁ || l и обозначим точку пересечения прямой l ₁ с плоскостью α через А₁. Точка А₁ называется проекциейточки А наплоскость α относительнопрямой l.

Если прямая l 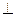α, то проекция называется прямоугольной, или ортогональной.

Определение. Углом между двумя векторами, или между осями, или между вектором и осью называется наименьший угол α, на который надо повернуть один из векторов или одну из осей до совпадения по направлению с другим вектором или осью.

Из определения следует, что 0 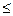α 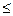π. Угол между векторами или между осями, или между вектором и осью будем обозначать соответственно: (), (), ().

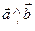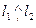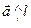Теорема. Проекция вектора на ось обладает следуицики свойствами:

1) ;

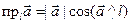2)

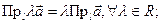
3) .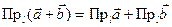