
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определители второго и третьего порядков
|
|
Определение. Таблица, составленная из чисел, записанных в следующем виде:
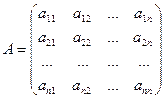
называется квадратной матрицей n-го порядка или просто матрицей n-го порядка. Первый индекс i элемента а ij матрицы А указывает на номер строки, а второй индекс j - на номер столбца, на пересечении которых стоит элемент аij.
Пусть дана квадратная матрица А второго порядка:
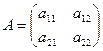
Определителем (детерминантом) матрицы А второго порядка называется число Δ равное:
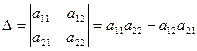
то а11а22> О, т.е. коэффициенты а11 и а22 оба отличны от нуля и имеют одинаковые знаки, совпадающие со знаком I1=a11+а22. Будем в дальнейшем считать, что I1> О, т.е. а11> 0 и а22> 0 (если это не так, то умножим обе части (18) на — 1). Заметим, что при такой операции (нормировании) знак I2 не меняется.
Теорема 1.3. Пусть уравнение (1) КВП — эллиптического типа (I2> О) нормировано так, что I1> О. Тогда при I3< 0 — это уравнение эллипса. При I3=0 — единственная точка (уравнение вырожденного эллипса). При I3> 0 — пустое множество точек (уравнение мнимого эллипса).
Доказательство. Так для уравнения (18), I1=а" 11+а" 22,
I2=а" 11а22, то из условия I1> О, I2> 0 следует, что а" 11> О, а" 22> 0. Поэтому уравнение (18) можно записать так:
 , при I3< 0; (19)
, при I3< 0; (19)
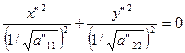 , при I3=0; (20)
, при I3=0; (20)
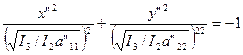 , при I3> 0; (21)
, при I3> 0; (21)
Теорема доказана.
Теорема 1.4. Пусть уравнение (1) - КВП гиперболического типа (I2< 0). Тогда при I3  0 — это уравнение гиперболы, а при I3=0 - пара пересекающихся прямых.
0 — это уравнение гиперболы, а при I3=0 - пара пересекающихся прямых.
Доказательство. Так как для уравнения (18):
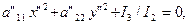

члена 2а'12х'у'. Ясно, что в этом случае а'12=0 и из формул (4) следует, что
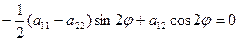
Следовательно, при а12  0
0
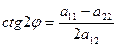 (16)
(16)
Именно при таком выборе угла поворота, уравнение (3) принимает вид:
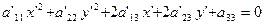 (17)
(17)
Вывод: путем параллельного переноса приводим уравнение кривой к виду (14)
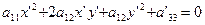
путем поворота, если а12  О, приводим уравнение (14) к виду:
О, приводим уравнение (14) к виду:
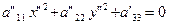 (17)
(17)
в системе координат О" Х" У".