
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямая на плоскости
|
|
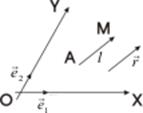 Пусть в плоскости α задана афинная система координат (0,
Пусть в плоскости α задана афинная система координат (0, 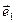 ,
, 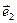 ) и прямая l, принадлежащая этой плоскости α. Составим уравнение прямой l. Заметим, что положение прямой l однозначно определено, если известен вектор, коллинеарный этой прямой и называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять любой вектор, коллинеарный данной прямой. Пусть
) и прямая l, принадлежащая этой плоскости α. Составим уравнение прямой l. Заметим, что положение прямой l однозначно определено, если известен вектор, коллинеарный этой прямой и называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять любой вектор, коллинеарный данной прямой. Пусть 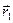 = (m1, n1) и
= (m1, n1) и 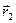 =(m2, n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов
=(m2, n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов
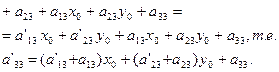 (7)
(7)
Тогда в новой системе координат O’X’Y’
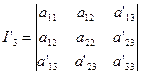
Вычтем из 3-ей строки 1-ю, умноженную на x0, и затем вторую,
умноженную на у0. Тогда
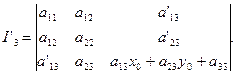
Теперь из 3-ro столбца вычтем 1-й, умноженный на x0 и второй, умноженный на y0. Получим, что I'3=I3.
Рассмотрим теперь преобразование поворота


Разложим I'3 по элементам 3-го столбца. Получим:
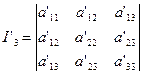 =
=
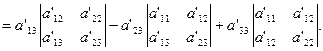 (8)
(8)
Распишем каждое из 3-х слагаемых в выражении (1.34), пользуясь формулами (1.31).
Если же А = 0, то α = 0 и в этом случае a12=(1/2)(а11—а22).
Введем также угол β, считая
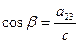 ,
, 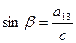 ,
,
если С  0. Если же С=0, т.е. а13=а23=0, то β =0.
0. Если же С=0, т.е. а13=а23=0, то β =0.
Тогда выражения (1.30) перепишутся в виде:
a'11=Азin(2φ +α)+В; а'12=Асоs(2φ +α);
a'22=—Азin(2φ +α)+В; a'13=Csin(φ +β); (5)
a'23= Ссоз(φ +β); а'33=а33.
Отметим, что величины А, В, С и углы α, β не зависят от φ.
Инварианты кривой второго порядка
Инвариантом уравнения (1) относительно преобразования системы координат ОХУ называется такая функция
f(а11, а12, a22, a13, а23, а33),
которая не меняется при переходе к новой системе координат 0'Х'У'. Таким образом, если f — инвариант, то f(a11,...а33) = f(a'11...а'33).
Теорема 1.2. Величины

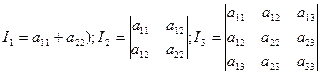 (6)
(6)
являются инвариантами уравнения (1) линии второго порядка
относительно преобразований декартовой системы координат.
Доказательство проведем вначале для преобразования параллельного переноса, а затем для преобразования поворота.
Инвариантность I1 и I2 следует из формул (2). Заметим, что из этих формул также следует, что
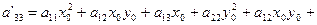
следует, что 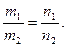 Если прямая l не параллельна оси OY, то
Если прямая l не параллельна оси OY, то  следовательно,
следовательно,
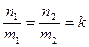
- угловой коэффициент относительно выбранной системы координат.
В частности, для прямоугольной системы координат (0, 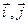 )
)
k = tgα, где α – угол между осью ОХ и любым направляющим вектором прямой l. Угол α называется углом наклона прямой l к оси ОХ.
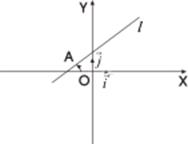
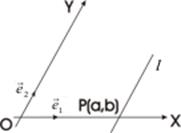
Если прямая l параллельна оси ОY, то l пересекает ось OХ в некоторой точке Р(а, 0). Тогда все точки прямой и только они удовлетворяют соотношению
x = a, Р(а, 0)
- уравнение прямой, проходящей через точку параллельно оси ОУ. Заметим, что в качестве направляющего вектора такой прямой можно взять вектор 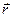 (0, р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует.
(0, р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует.
Пусть прямая l проходит через точку A (а, b) и имеет угловой коэффициент k. Возьмем произвольную точку М (х, у) на прямой l. Тогда 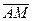 =(х - а, у - b) - направляющий вектор прямой l.
=(х - а, у - b) - направляющий вектор прямой l.
Следовательно,
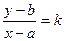
Отсюда
y – b = k (x - а)
-уравнение прямой с угловым коэффициентом k.