Координаты на плоскости.

Пусть на плоскости α заданы две координатные оси ОХ и OY с

неколлинеарными ортам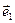и и 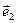cоответственно. Тогда тройка (О, 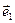, 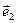) называется афинным репером, или афинной системой координат плоскости α.

Точка 0 называется началом кооpдинат, векторы 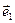и 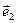- базисными векторами. Если М – произвольная точка на плоскости α, то

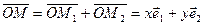
Числа х и у называются афинными координатами точки М в системе (0, 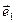, 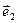), причем х называется абсциссой, а у – ординатой

(записывается: М(х, у)). Вектор 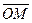называется радиус-вектором точки М, числа х, у - координатами вектора ОМ (записывается: ОМ=(х, у)).

Афинная система координат (0, 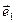, 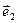) обозначается также OXY. Ось ОХ называется осью абсцисс, ось OY - осью ординат.

Теорема. Пусть = 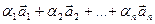, где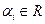

.

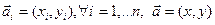Тогда

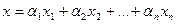
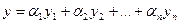
Следствие 1. Пусть даны точки А (х ₁, y ₁) и В (х ₂, у ₂).

Тогда

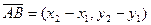
Следствие 2. Два вектора = (х ₁, у ₁) и = (х ₂, у ₁) коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, то есть

.

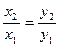Афинная система координат (0, 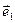, 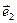), в которой орты 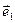и 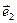взаимно ортогональны, называется декартовой, или прямоугольной системой координат. В этом случае орты 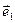и 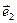обозначаются соответственно 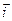и 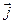.