Основная теорема о поверхностях второго порядка

Определение. Поверхностью второго порядка (ПВП) называется множество всех точек пространства, которые в прямоугольной системе координат удовлетворяют уравнению:

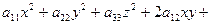
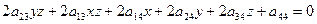(1)

Теорема. Для любой поверхности второго порядка существует прямоугольная система координат OXYZ, в которой уравнение(1) имеет один из следующих 17 видов:

1) эллипсоид:

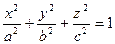
2 ) мнимый эллипсоид:

+

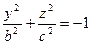
3) однополостный гиперболоид:

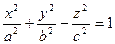
Доказательство. Итак, для уравнения (1)

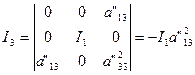(28)

Так как I₁ О, то при I₃ 0 следует, что а" ₁₃ О, а при I₃=0 получаем, что а" ₁₃=О. Тогда уравнение (27) можно записать так

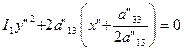при I₃ О, (29)

при I₃=О, 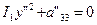(30)

Очевидно, что уравнение (29) — уравнение параболы. Чтобы

оно стало каноническим, достаточно осуществить параллельный перенос системы координат 0" Х" У":

y" =Y;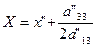

и обозначить – а " ₁₃/I₁=р. Тогда в системе координат ОХУ получаем уравнение

У² = 2рХ.

Уравнение (30) можно записать так:

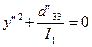(31)

Тогда, если a" ₃₃/I₁< 0, то из (31) получаем

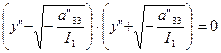
линеарен вектору 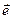и, значит, 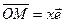. Вектор 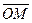называется радиус-вектором точки М, а число х называется координатойточки М на координатной оси l (обозначается: М(х)) или координатой радиус-вектора 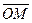(обозначается: 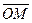=(х)).

Так как 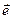- единичный вектор, то каждой точке М на оси l поставлено в соответствие вполне определенное действительное число – ее координата.

Обратно, для каждого действительного числа х найдется единственная точка М оси l, координата которой равна х. Таким образом, положение любой точки координатной оси однозначно определяется заданием координаты этой точки.