
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные операции над векторами.
|
|
Определение. Суммой  +
+  векторов
векторов  и
и  называется вектор, проведенный из начала
называется вектор, проведенный из начала  к концу
к концу  , если конец
, если конец  и начало
и начало  совпадают. Приведенное определение сложения векторов называется правилом треугольника. Векторы
совпадают. Приведенное определение сложения векторов называется правилом треугольника. Векторы  и
и  можно складывать, пользуясь правилом параллелограмма.
можно складывать, пользуясь правилом параллелограмма.
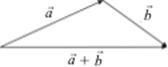
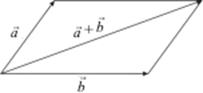
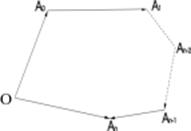
Если имеется n векторов 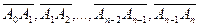 , то их сумма определяется как вектор
, то их сумма определяется как вектор 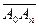 .
.
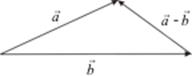
Определение. Разностью векторов  и
и  называется такой вектор
называется такой вектор 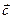 =
=  -
-  , что выполняется равенство
, что выполняется равенство 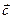 +
+  =
=  .
.
Легко показать, что для любого вектора  , существует такой единственный вектор
, существует такой единственный вектор  , называемый противоположным вектору
, называемый противоположным вектору 
что  +
+  =
= 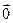 . Вектор, противоположный вектору
. Вектор, противоположный вектору  , будем обозначать –
, будем обозначать –  .
.
Определение. Произведением вектора  на число λ (λ
на число λ (λ  0) называется вектор
0) называется вектор  =λ
=λ  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) векторы  и
и  одинаково направлены, если λ > 0, и противоположно направлены, если λ < 0;
одинаково направлены, если λ > 0, и противоположно направлены, если λ < 0;
2) |  |=|λ ||
|=|λ ||  |.
|.
По определению, произведение произвольного вектора  на число 0 есть нулевой вектор, т.е. 0
на число 0 есть нулевой вектор, т.е. 0  =
= 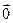 .
.
Введенные операции сложения векторов и умножение вектора на число называются линейными. Они обладают следующими свойствами:
1) сложение векторов коммутативно:
 +
+  =
=  +
+  , "
, "  ,
,  ;
;
2) сложение векторов ассоциативно:
( +
+  )+
)+ 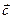 =
=  +(
+( +
+ 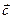 ), "
), "  ,
,  ,
, 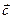 ;
;
3)  +
+ 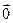 =
=  , "
, "  ;
;
4)  +(-
+(-  )=0, "
)=0, "  ;
;
5) умножение вектора на число ассоциативно:
α (β  ) = (α β)
) = (α β)  , "
, "  " α, β Î R;
" α, β Î R;
6) 1  =
=  , "
, "  ;
;
7) умножение вектора на число дистрибутивно по отношению к
сложению чисел:
(α +β)  =α
=α  +β
+β  , "
, "  , " α, β Î R;
, " α, β Î R;
8) умножение вектора на число дистрибутивно по отношению к сложению векторов:
α ( +
+  )=α
)=α  +α
+α  , "
, "  ,
,  , " α Î R;
, " α Î R;
Множество всех векторов пространства (плоскости), удовлетворяющих свойствам 1) – 8), называется линейным, или векторным пространством, и обозначается 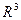 (
(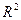 ).
).
Теорема (необходимое и достатаочное условие коллинеарности двух векторов). Для того чтобы векторы  и
и  были коллинеарны, необходимо и достаточно, чтобы существовало λ, удовлетворяющее условию:
были коллинеарны, необходимо и достаточно, чтобы существовало λ, удовлетворяющее условию:
 = λ
= λ  .
.