Работа и кинетическая энергия

Расширяя ньютоновский язык описания движения, мы вводим новую меру движения, называемую кинетической энергией (KE), которая определяется формулой:

(5.1)

Как мы скоро увидим, множитель 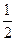в формуле (5.1) появляется, подобно тому, как и в формуле Галилея для равноускоренного движения.

Определение кинетической энергии выглядит обманчиво похожим на определение импульса, но факт, что в нем скорость возводится в квадрат, имеет решающее значение. Именно это делает кинетическую энергию ненаправленной (скалярной) мерой движения. Положительна ли скорость или отрицательна, ее квадрат всегда положителен. Движения в противоположных направлениях не уравновешиваются!

Второй шаг определяет величину, называемую работой. Работа — мера изменения энергии под действием силы. Работа вычисляется перемножением силы F и расстояния, s, на котором тело движется строго в направлении действия силы. Например: если сила — сила тяжести, то мы учитываем только вертикальное перемещение движущего тела. Это определение работы наиболее просто выражается математической формулой, содержащей тригонометрическую функцию косинус.

(5-2)

где 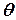— угол между силой и направлением движения.

Даже если Вы не очень дружите с тригонометрией, смысл формулы (5-2) легко объяснить. Если сила направлена вперёд, то 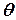меньше чем 90°. Для таких углов косинус положителен. Для углов от 90° до 180° косинус отрицателен. Для угла 90° косинус равен нулю, и, таким образом, никакая работа не совершается. А ведь это именно то, что мы потребовали в п. 2 предыдущего раздела!

Чтобы проиллюстрировать использование понятий работы и кинетической энергии, рассмотрим тело, которое начинает двигаться из состояния покоя под действием постоянной силы. Оно может двигаться только в направлении силы, так что угол 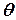=0°, а его косинус равен единице. Таким образом, работа — это просто .

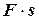Движение тела происходит с постоянным ускорением, так что складывается точно такая же ситуация, что описана в Главе1. Значит, можно использовать формулу 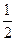для вычисления перемещения. Мы также можем использовать второй закон Ньютона и заменить силу произведением . Тогда мы имеем:

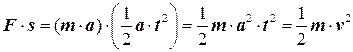
Этот пример, адресованный тем, кто не боится математики, показывает, что совершенная силой работа равна появившейся у тела кинетической энергии.

Рассмотрим теперь автомобиль, движущийся с постоянной скоростью. В этом случае сила, производимая двигателем, тоже совершает работу, но эта работа не приводит к увеличению кинетической энергии. Дело в том, что сила, производимая двигателем, уравновешена трением и сопротивлением воздуха. Работа, совершенная этой силой, однако, не теряется — она переходит в другие формы энергии. А это как раз именно то, что мы зафиксировали в п. 3 предыдущего раздела!

Можем ли мы вернуть свои деньги?

Все те преобразования энергии, которые мы успели рассмотреть, были сопряжены с существенными изменениями в окружающем мире: сгорает бензин, нагреваются тормоза и т.д. Однако с некоторыми силами, и особенно с силой тяжести, происходит что-то таинственное. Падающий камень приобретает энергию, при своем падении. Откуда эта энергия? Ведь ничего, кроме местоположения камня не меняется!

Ответ на этот вопрос помогает найти пример, показанный на рис. 5 - 1. С точки зрения энергии — это свободное падение “наоборот”, поскольку при подъёме камня с помощью лебёдки энергия расходуется без какого-либо видимого результата, кроме изменения в положении камня.

Снова, с ньютоновской точки зрения ничего интересного здесь не происходит.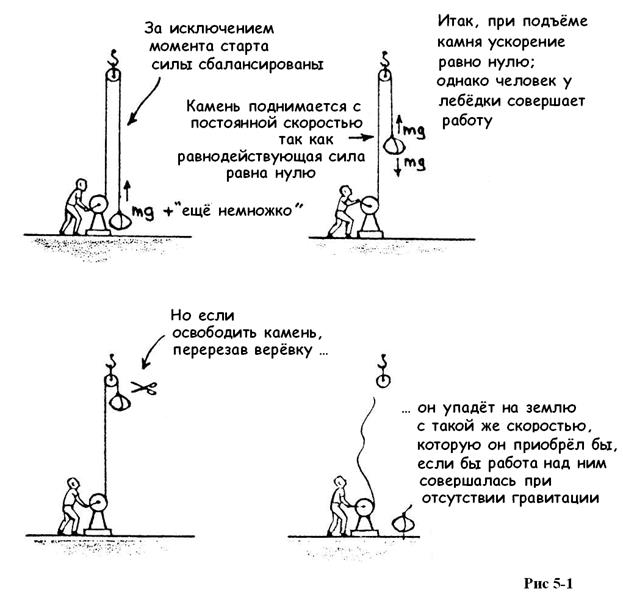
На большей части своего пути “вверх” камень движется с постоянной скоростью — его вес, точно уравновешен силой натяжения веревки. Правда, для того, чтобы привести камень в движение должен существовать краткий момент, когда сила натяжения верёвки превышает вес камня, но после этого движение камня равномерно. В терминах законов Ньютона это означает, что камень может и вообще остановиться. А вот с точки зрения человека, работающего за лебёдкой, различие есть, и весьма значительное. Да, он может остановить подъём груза, поставить лебёдку на тормоз и уйти. Но это не поднимет камень — для дальнейшего подъёма придется ещё попотеть, развивая мышечные усилия и совершая работу. Эта работа — произведение веса mg на расстояние h — не идет на увеличение кинетической энергии камня. Так что же, эта работа потеряна навсегда?

Ответ: конечно же, нет! Если перерезать веревку, то камень начнет падать. Сила тяжести действует на камень, и он достигнет поверхности земли с кинетической энергией, равной работе силы тяжести. Таким образом, камень будет двигаться с такой же скоростью, которую он приобрел бы, если бы затраченная работа была совершена над ним в отсутствии силы тяжести.

Энергию, " запасенную" таким образом называют потенциальной энергией. Смысл слова очевиден. Поднимая камень, мы создали ситуацию, которая потенциально может создать движение. Перерезав верёвку, мы преобразуем этот потенциал в реальное движение.

Процесс преобразования потенциальной энергии в кинетическую энергию является постепенным. Когда камень проделал только одну десятую часть своего пути к земле, то сила тяжести совершила только одну десятую часть своей работы. Одна десятая часть энергии стала кинетической, другие девять десятых частей остаются потенциальными. Поскольку камень продолжает свое падение, потенциальная энергия постепенно расходуется, а кинетическая — увеличивается. Когда камень достигнет земли, вся потенциальная энергия будет преобразована в кинетическую, и работа, затраченная на подъем камня, проявит себя как кинетическая энергия камня.

Эти отношения могут быть выражены математически в форме

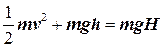(5-4)

где h — высота на которой находится падающий камень, а Н — высота, с которой он начал своё падение. С помощью этой формулы для любой высоты h мы можем вычислить скорость камня, поскольку его кинетическая энергия — это разность между mgH и mgh.

Но ведь Галилей делал то же самое, не пользуясь понятиями кинетической и потенциальной энергии.

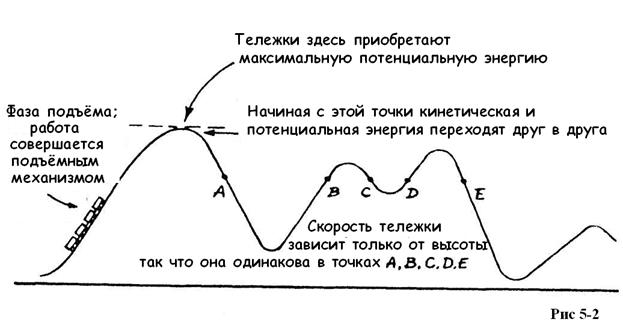
Да, действительно, если бы уравнение (5-4) было применимо только к падающему камню, то его вряд ли стоило бы даже записывать. Но рассмотрим аттракцион, схематически изображенный на рис. 5 - 2 [5]. Формула (5-4) применима и в этой ситуации. Как только тележка поднята на вершину первого возвышения и отпущена, она движется под действием только двух сил: силы тяжести и силы реакции рельс. Однако последняя всегда перпендикулярна движению, и, следовательно, не совершает никакой работы. Скорость, которую приобретает тележка в разных точках этого извилистого рельефа, зависит только от высоты этой точки над основанием и совпадает со скоростью тела, свободно падающего с высоты Н[6].