Луна как связь земного и небесного.

Однако законы Кеплера говорят только об относительных скоростях движения разных планет, или о скоростях одной планеты в разных точках её орбиты. Не зная ни величины силы, действующей на планету, ни массы Солнца, ни коэффициента γ в формуле 4-1, не было возможности завершить анализ: Ньютон продемонстрировал, что его закон может объяснить, почему год на Марсе вдвое длиннее года на Земле, но длину самого года вычислить не мог. Так что простое объяснение законов Кеплера не могло разрушить дихотомию (раздвоение) между явлениями земными и небесными.

К счастью для Ньютона, наша Земля имеет спутник, Луну. Так как одна и та же Земля создаёт ускорение свободного падения камня и ускорение Луны на её орбите, то единственное отличие этих двух явлений состоит в том, что Луна находится много дальше от центра Земли, и поэтому изменение силы гравитации можно подсчитать. По измеренному ускорению камня на поверхности Земли можно рассчитать, какое ускорение должна иметь на своей орбите Луна, если она подвержена действию только силы гравитации Земли. Будет ли соответствовать этот расчёт наблюдаемому движению Луны? Здесь для Ньютона открывалась возможность прямого количественного доказательства того, что одна и та же сила вызывает движения и камня, и Луны.

Уже во времена Ньютона расстояние до Луны было известно, т.к. его довольно легко измерить. Оно составляет 380000 км, что в 60 раз больше радиуса Земли. Таким образом, ускорение под действием силы гравитации Земли на лунной орбите должно быть в (60)² раз меньше, чем ускорение свободного падения на Земле, то есть:

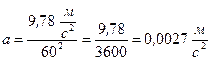
Если мы примем, что движение Луны является движением материального объекта под действием одной только силы земного тяготения, то «а» должно быть ускорением на её орбите.

Остаётся подсчитать наблюдаемое ускорение Луны, используя формулу, полученную в предыдущей главе. Скорость Луны на её орбите равна 1016 мс^-1. Она получена делением длины орбиты 2π ·380000 км на длину лунного месяца 27, 32 дня. Таким образом, искомое ускорение получается

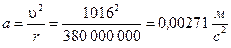
Учитывая тот факт, что орбита Луны не совсем круговая, а слабо эллиптическая, соответствие двух величин ускорения «а» является просто великолепным.

Чтобы убедиться, что мы не потеряли нить рассуждений, занимаясь арифметикой, резюмируем сказанное. Итак, мы начали с предположения, что Луна, являясь материальным объектом, подчиняется тем же законам, которые действуют на Земле. Мы обнаружили, что ускорение Луны меньше ускорения свободного падения тела на Земле ровно во столько раз, во сколько отличаются квадраты их расстояний от центра Земли.

Этот результат был шокирующим. Конечно, один такой результат может оказаться простым совпадением, и окончательное доказательство ещё впереди и потребует более детальных расчётов других явлений. И всё же приведённый расчёт был прочной связью и количественной корреляцией между явлением на Земле и явлением на небесах.

Но самый главный аспект теории оставался не доказанным: её претензия на открытие универсальной силы, которая действует между любыми телами на любом расстоянии и пропорциональна произведению их масс. По законам Кеплера можно было убедиться, что сила притяжения Солнца, обратно пропорциональная квадрату расстояния, объясняет движение всех планет Солнечной системы (включая Землю). Подобная сила, создаваемая Землёй, объясняет движение всех падающих тел и движение Луны вокруг Земли. Однако, не зная масс Солнца и Земли, Ньютон имел слабые основания для утверждения, что сила пропорциональна массе большего «центрального» объекта в каждом из упомянутых случаев. И он не имел никаких оснований утверждать, что эта сила может действовать и, например, между двумя камнями на Земле, разве что мог утверждать, что земные камни взаимодействуют слишком слабо, чтобы это можно было измерить. Тем не менее, достижения теории тяготения были столь убедительны, и они так хорошо соответствовали духу ньютоновской физики, что немногие физики серьёзно сомневались в универсальности теории с момента её публикации. Универсальность теории тяготения не имела прямого подтверждения, пока полтора столетия спустя Генри Кавендиш не изобрёл прибор для измерения слабого взаимодействия двух тел в лаборатории. Вера в закон гравитации Ньютона была столь велика, что Кавендиш назвал свой эксперимент не «подтверждением закона Всемирного тяготения», а «взвешиванием Земли»; это название также опиралось на недоказанное утверждение, что сила земного тяготения, действующая на камень, пропорциональна массе Земли, также как и массе камня. Так как он измерил силу между двумя объектами известных масс, Кавендиш впервые получил в свои руки всю информацию, необходимую для вычисления гравитационной постоянной γ в формуле Ньютона. Как только эта константа стала известной, вес известной массы (конкретного тела) на Земле можно было использовать для расчета массы Земли, так как все остальные члены в формуле для силы известны.

По крайней мере в течение столетия после публикации «Принципов», самым важным приложением и подтверждением ньютоновских законов механики и гравитации оставались расчеты движений планет. И только в XIX веке, когда создание машин перестало, наконец, быть процессом проб и ошибок, ньютоновские законы движения получили своё практическое применение.