
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 6
|
|
ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ
Некоторые детали имеют элементы, равномерно
расположенные по окружности, например, детали на рис. 52 … 59. При выполнении чертежей подобных деталей необходимо уметь делить окружность на равные части.
Деление окружности на четыре и восемь равных частей. На рис. 52, а показана крышка, в которой имеется восемь отверстий, равномерно
расположенных по окружности. При построении
чертежа контура крышки (рис. 52, г) необходимо
разделить окружность на восемь равных частей.
Два взаимно перпендикулярных диаметра окружности делят ее на четыре равные части (точки 1, 3, 5, 7 на рис. 52, б). Чтобы разделить окружность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2, 4, 6, 8. Это можно сделать с помощью угольника с углами 45° (рис. 52, в), гипотенуза угольника должна проходить через центр окружности, или построением.
Деление окружности на три, шесть и двенадцать равных частей. Во фланце (рис. 53, а) имеется три отверстия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 53, г) нужно разделить окружность на три равные части.
Для нахождения точек, делящих окружность радиуса R на три равные части, достаточно из
любой точки окружности, например точки А, провести дугу радиусом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки А, с окружностью (рис. 53, б).
Разделить окружность на три равные части можно также угольником с углами 30 и 60° (рис. 53, в), гипотенуза угольника должна проходить через центр окружности.
На рис. 54, б показано деление окружности циркулем на шесть равных частей. В этом случае выполняется то же построение, что на рис. 53, б, но дугу описывают не один, а два раза, из точек / и 4 радиусом R, равным радиусу окружности.
Разделить окружность на шесть равных частей можно и угольником с углами 30 и 60° (рис. 54, в). На рис. 54, а показана крышка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.
Чтобы выполнить чертеж детали (рис. 55, а), которая имеет 12 отверстий, равномерно расположенных по окружности, нужно разделить окружность на 12 равных частей (рис. 55, г).
При делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 54, б), но дуги радиусом R
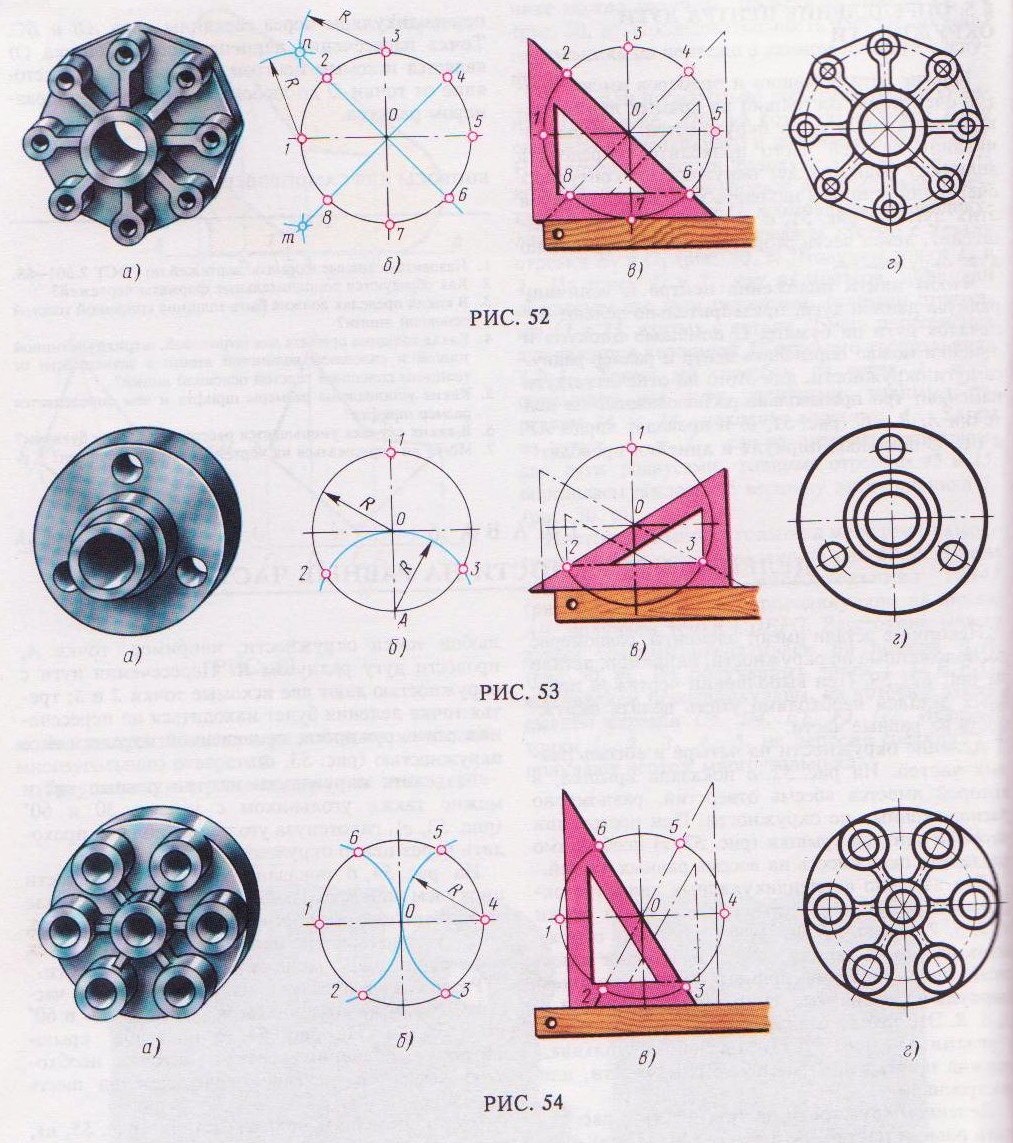
описывать четыре раза из точек 1, 7, 4 и 10 равных частей. В плашке (рис. 56, а) имеется
(рис. 55, б). пять отверстий, равномерно расположенных
Используя угольник с углами 30 и 60° с после- по окружности. Выполняя чертеж плашки
дующим поворотом его на 180°, делят окружность (рис. 56, в), необходимо разделить окружность на
на 12 равных частей (рис. 55, в). пять равных частей. Через намеченный центр О
Деление окружности на пять, десять и семь (рис. 56, б) с помощью рейсшины и угольника
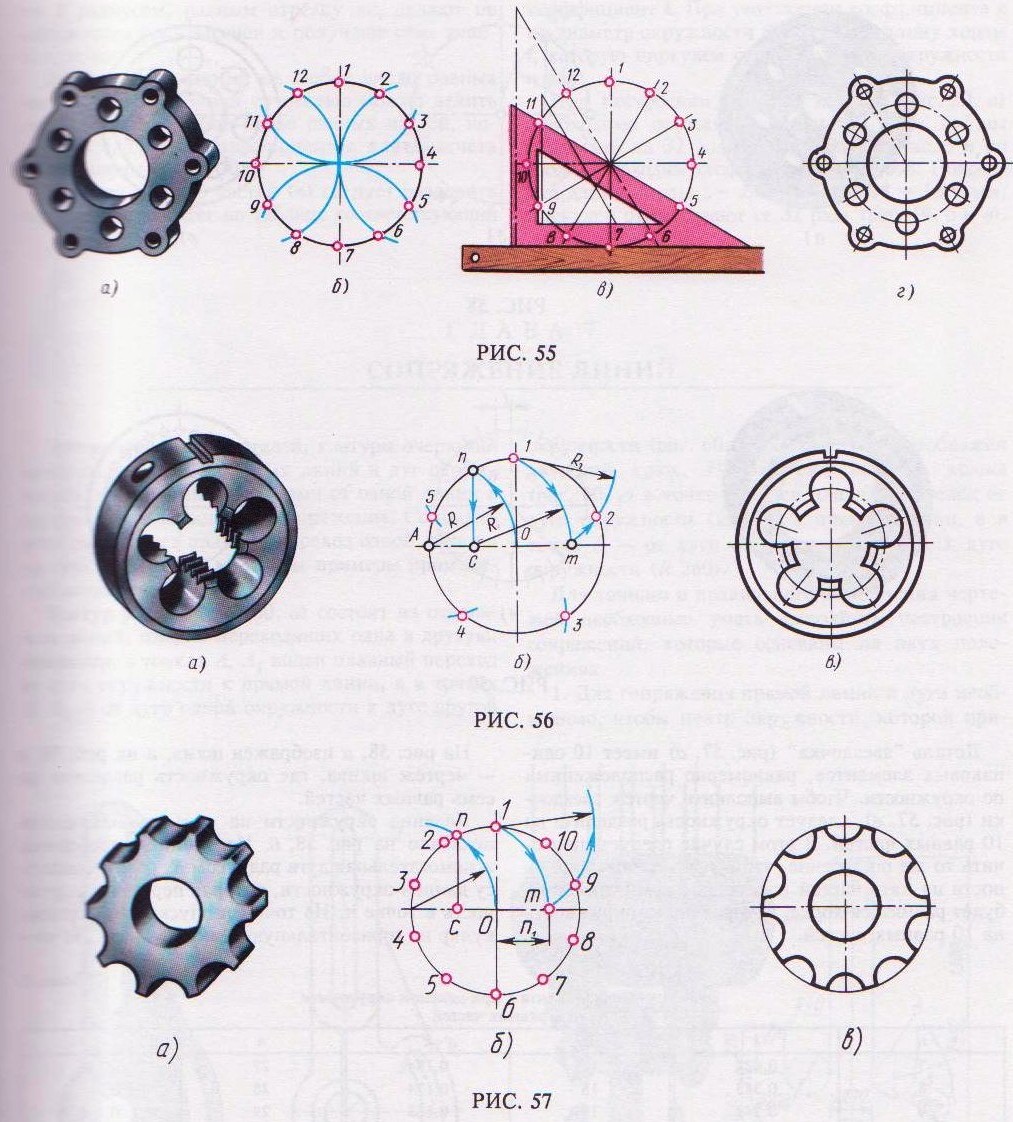
проводят осевые линии и из точки О циркулем описывают окружность заданного диаметра. Из точки А радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n опускают перпендикуляр на горизонтальную осевую линию, получают точку С радиусом R1 , равным
расстоянию от точки С до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке т. Из точки 1 радиусом R2, равным расстоянию от точки 1 до точки т, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1/5 длины окружности. Точки 3, 4 и 5 находят, откладывая циркулем отрезки, равные m1.
Деталь " звездочка" (рис. 57, а) имеет 10 одинаковых элементов, равномерно расположенных по окружности. Чтобы выполнить чертеж звездочки (рис. 57, в), следует окружность разделить на 10 равных частей. В этом случае следует применить то же построение, что и при делении окружности на пять частей (см. рис. 56, б). Отрезок n1 будет равняться хорде, которая делит окружность на 10 равных частей.
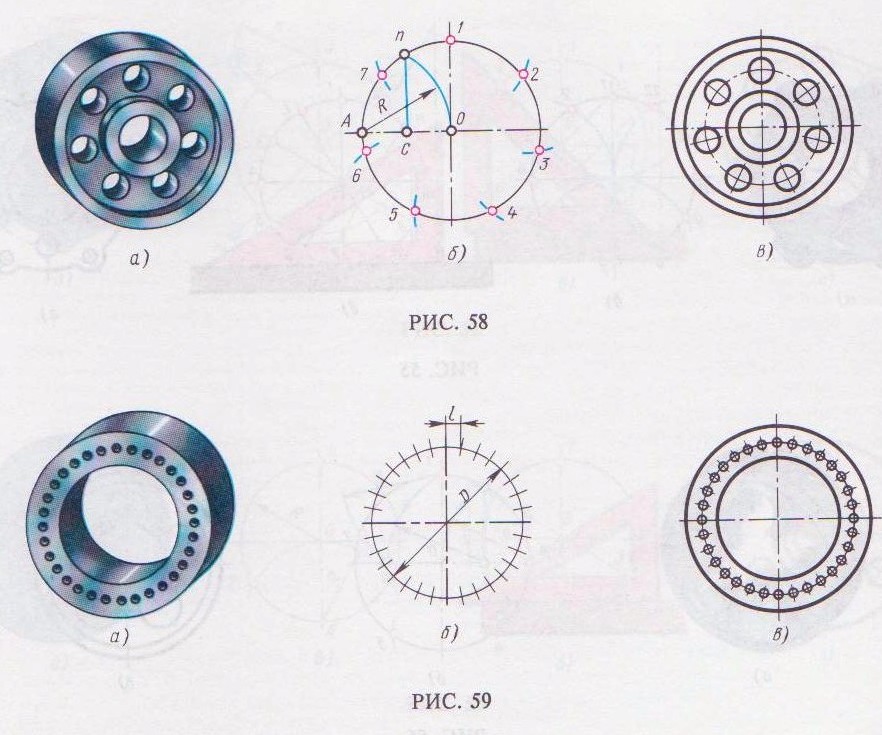
На рис. 58, а изображен шкив, а на рис. 58, в – чертеж шкива, где окружность разделена на семь равных частей.
Деление окружности на семь равных частей показано на рис. 58, б. Из точки А проводится вспомогательная дуга радиусом R, равным радиусу данной окружности, которая пересечет окружность в точке п. Из точки п опускают перпендикуляр на горизонтальную осевую линию. Из точ-
Таблица 10
Значение коэффициента k при делении окружности на n равных частей
| п | k | п | k | п | k |
| 0, 434 | 0, 184 | 0, 116 | |||
| 0, 383 | 0, 174 | 0, 112 | |||
| 0, 342 | 0, 165 | 0, 108 | |||
| 0, 309 | 0, 156 | 0, 104 | |||
| 0, 282 | 0, 149 | 0, 101 | |||
| 0, 259 | 0, 142 | 0, 098 | |||
| 0, 239 | 0, 136 | 0, 095 | |||
| 0, 223 | 0, 130 | 0, 092 | |||
| 0, 208 | 0, 125 | 0, 900 | |||
| 0, 195 | 0, 120 | 0, 087 |
ки 1 радиусом, равным отрезку nc, делают по окружности семь засечек и получают семь искомых точек.
Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 10).
Зная, на сколько частей (n) следует разделить окружность, находят по таблице соответствующий коэффициент k.
При умножении коэффициента k на диаметр окружности D получают длину хорды l, которую циркулем откладывают на окружности п раз.
При построении чертежа кольца (рис. 59, а) необходимо окружность диаметра D = 142 мм разделить на 32 равные части. Зная число n, по таблице находим коэффициент k= 0, 098. Подсчитав длину хорды l = Dk = 142x0, 098 = 13, 9 мм, циркулем откладывают ее 32 раза (рис. 59, б и в).