Изображение взаимного положения двух прямых на комплексном чертеже

Из курса начертательной геометрии известно что:

а) если прямые параллельны в пространстве
то их одноименные проекции параллельны
(рис. 98, а);

б) если прямые пересекаются в точке А, то их одноименные проекции тоже пересекай
(рис. 98, б); при этом проекции точки пересе-

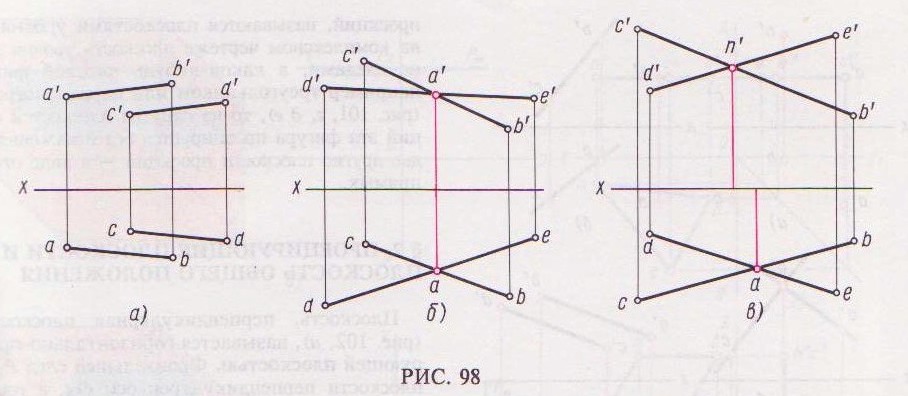
чения А обязательно располагаются на одном перпендикуляре к оси (на одной линии связи);

в) если точки пересечения проекций прямых, например, п' и а не расположены на одном перпендикуляре к оси х (рис. 98, в), то прямые скрещиваются.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Какие прямые называются прямыми общего положения?

2. Назовите основные плоскости проекций.

3. Что такое комплексный чертеж и каковы правила его по­строения?

4. Назовите возможные относительные положения двух пря­мых линий.

5. Дайте определение горизонтально-, фронтально- и про­фильно-проецирующей прямой.

6. Что называется следом прямой?

ГЛАВА 14

ПРОЕЦИРОВАНИЕ ПЛОСКИХ ФИГУР

§1. ИЗОБРАЖЕНИЕ ПЛОСКОСТИ ОМПЛЕКСНОМ ЧЕРТЕЖЕ

Плоскостью называется поверхность, образуемая движением прямой линии, которая движется параллельно самой себе по неподвижной направляющей прямой (см. рис. 89, б и в).

Проекции плоскости на комплексном чертеже

будут различны в зависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана: а) тремя точками, не лежащими на одной прямой; б) прямой линией и точкой, лежащей этой прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми.

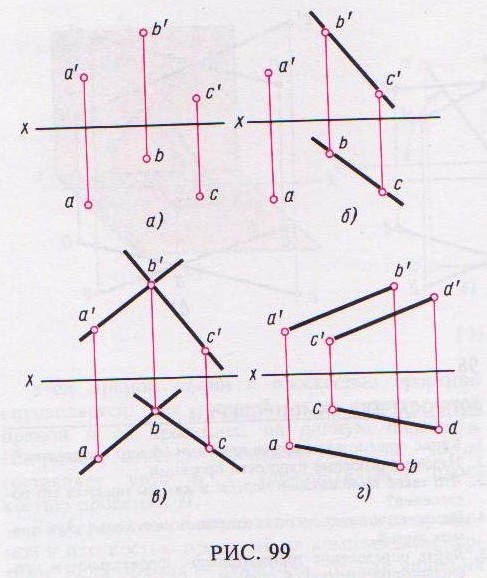
На комплексном чертеже (рис. 99) плоскости задаются аналогично, например, на рис. 99, а – проекциями трех точек А, В и С, не лежащих на одной прямой; на рис. 99, б – проекциями прямой ВС и точки А, не лежащей на этой прямой; на рис. 99, в – проекциями двух пересекающихся прямых на

рис. 99, г – проекциями двух параллельных

прямых линий АВ и CD.

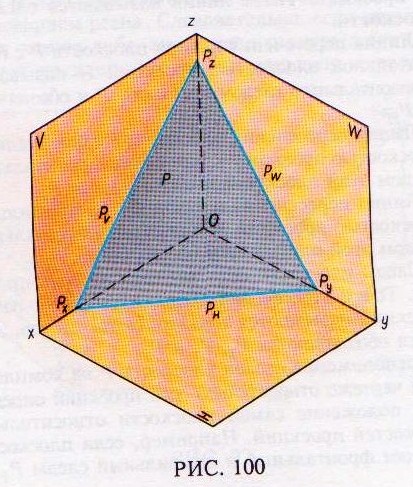
На рис. 100 плоскость задана прямыми линия­ми, по которым эта плоскость пересекает плоскос­ти проекций. Такие линии называются следами плоскости.

Линия пересечения данной плоскости Р с гори­зонтальной плоскостью проекций Н называется горизонтальным следом плоскости Р и обозначается Р_Н.

Линия пересечения плоскости Р с фронтальной плоскостью проекций V называется фронтальным следом этой плоскости и обозначается Р_V.

Линия пересечения плоскости Р с профильной плоскостью проекций W называется профильным следом этой плоскости и обозначается P_W.

Следы плоскости пересекаются на осях проек­ций. Точки пересечения следов плоскости с осями проекций называются точками схода следов. Эти точки обозначаются Р_х, Р_y и P_z.

Расположение следов плоскости Р на комплек­сном чертеже относительно осей проекций опреде­ляет положение самой плоскости относительно плоскостей проекций. Например, если плоскость Р имеет фронтальный и профильный следы P_V и

P_w, параллельные осям Ох и Оу, то такая плос­кость параллельна плоскости Н и называется го­ризонтальной (рис. 101, а). Плоскость Р со следа­ми Р_H и P_W, параллельными осям проекций Ох и Oz (рис. 101, б), называется фронтальной, а плос­кость Р со следами P_V и Р_H, параллельными осям проекций Оу и Oz, – профильной (рис. 101, в).

Горизонтальная, фронтальная и профильная плоскости, перпендикулярные двум плоскостям

проекций, называются плоскостями уровня. Если на комплексном чертеже плоскость уровня задана не следами, а какой-нибудь плоской фигурой, например треугольником или параллелограммом (рис. 101, г, д, е), то на одну из плоскостей проек­ций эта фигура проецируется без искажения, а на две другие плоскости проекций – в виде отрезков прямых.