Проецирующие плоскости и плоскость общего положения

Плоскость, перпендикулярная плоскости Н (рис. 102, а), называется горизонтально-проеци­рующей плоскостью. Фронтальный след P_V этой плоскости перпендикулярен оси Ох, а горизон­тальный след Р_H расположен под углом к оси Ох (комплексный чертеж на рис. 102, а).

Если горизонтально-проецирующая плоскость задана не следами, а какой-либо фигурой, напри­мер треугольником ABC (рис. 102, б), то горизон­тальная проекция этой плоскости представляет собой прямую линию, а фронтальная и профиль­ная проекции – искаженный вид треугольника ABC.

Фронтально-проецирующей плоскостью назы­вается плоскость, перпендикулярная фронтальной плоскости проекций (рис. 102, в).

Горизонтальный след этой плоскости перпенди­кулярен оси Ох, а фронтальный след расположен под некоторым углом к оси Ох (комплексный чертеж на рис. 102, в).

При задании фронтально-проецирующей плос­кости не следами, а, например, параллелограммом ABCD фронтальная проекция такой плоскости, представляет собой прямую линию (рис, 102, г а на горизонтальную и профильную плоскость проекций параллелограмм проецируется с искаже­нием.

Профильно-проецирующей плоскостью назы­вается плоскость, перпендикулярная плоскости (рис. 102, д). Следу P_V и Р_H этой плоскости параллельны оси Ох.

При задании профильно-проецирующей плос­кости не следами, а, например, треугольника- ABC (рис. 102, ё) профильная проекция такой плоскости представляет собой прямую линию. Плоскости, перпендикулярные двум плоское проекций, как было сказано, называются плоскос­тями уровня.

Если плоскость Р не перпендикулярна ни одной из плоскостей проекций (рис. 102, ж), то такая плоскость называется плоскостью общего поло­жения. Все три следа P_V, P_H и P_W плоскости наклонены к осям проекций.

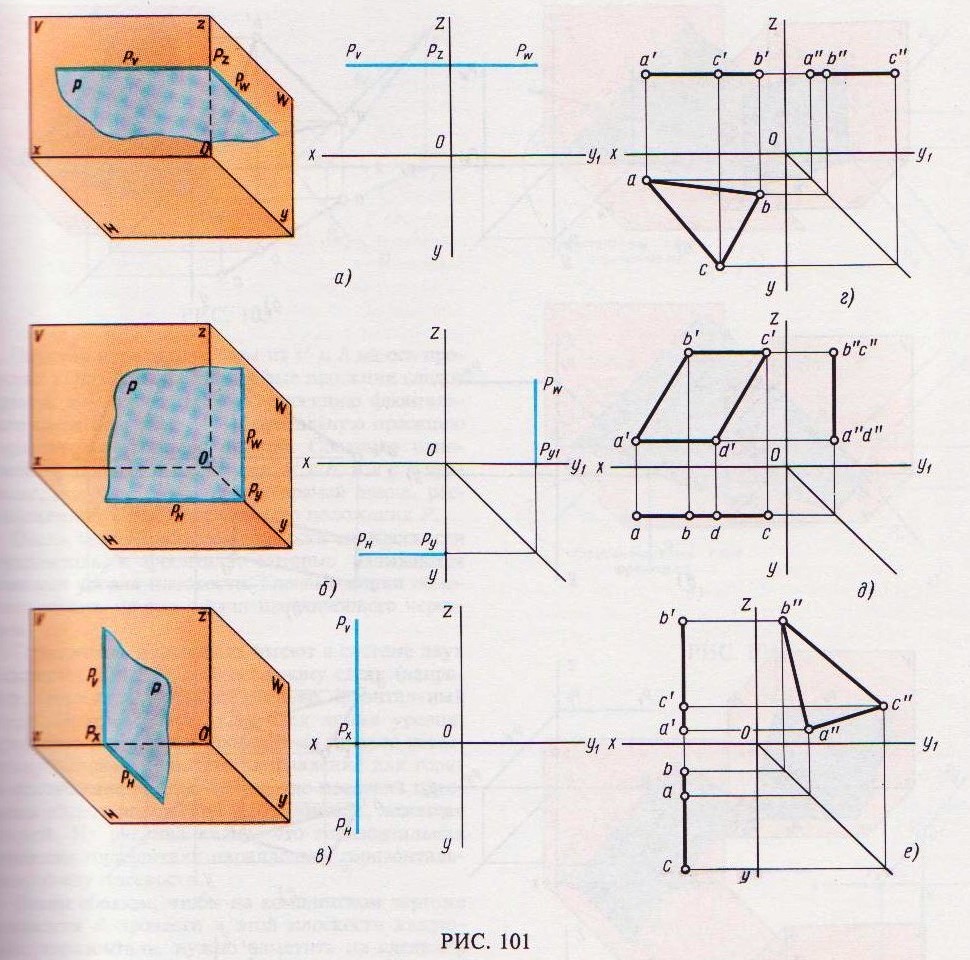
Если плоскость общего положения задана не а, например, треугольником ABC (рис. 102, з), то этот треугольник проецируется на плоскости Н, V и W в искаженном виде.

§ 3. ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, СЛОЖЕННЫХ НА ПЛОСКОСТИ

Если прямая расположена на плоскости, то она должна проходить через две какие-либо точки, принадлежащие этой плоскости. Такие две точки могут бытъ взяты на следах плоскости – одна на горизонтальном, а другая на фротальном. Так

как следы прямой и плоскости находятся на плос­костях проекций Н и V, то следы прямой, при­надлежащей плоскости, должны быть располо­жены на одноименных следах этой плоскости (рис. 103, а); например, горизонтальный след Н прямой – на горизонтальном следе Р_Н плоскости, фронтальный след V прямой – на фронтальном следе Р_V плоскости (рис. 103, б).

Для того чтобы на комплексном чертеже плос­кости Р, заданной следами, провести какую-либо прямую общего положения, необходимо наметить на следах плоскости точки v' и h и считать их следами искомой прямой (точнее, v' – фронталь­ной проекцией горизонтального следа прямой).

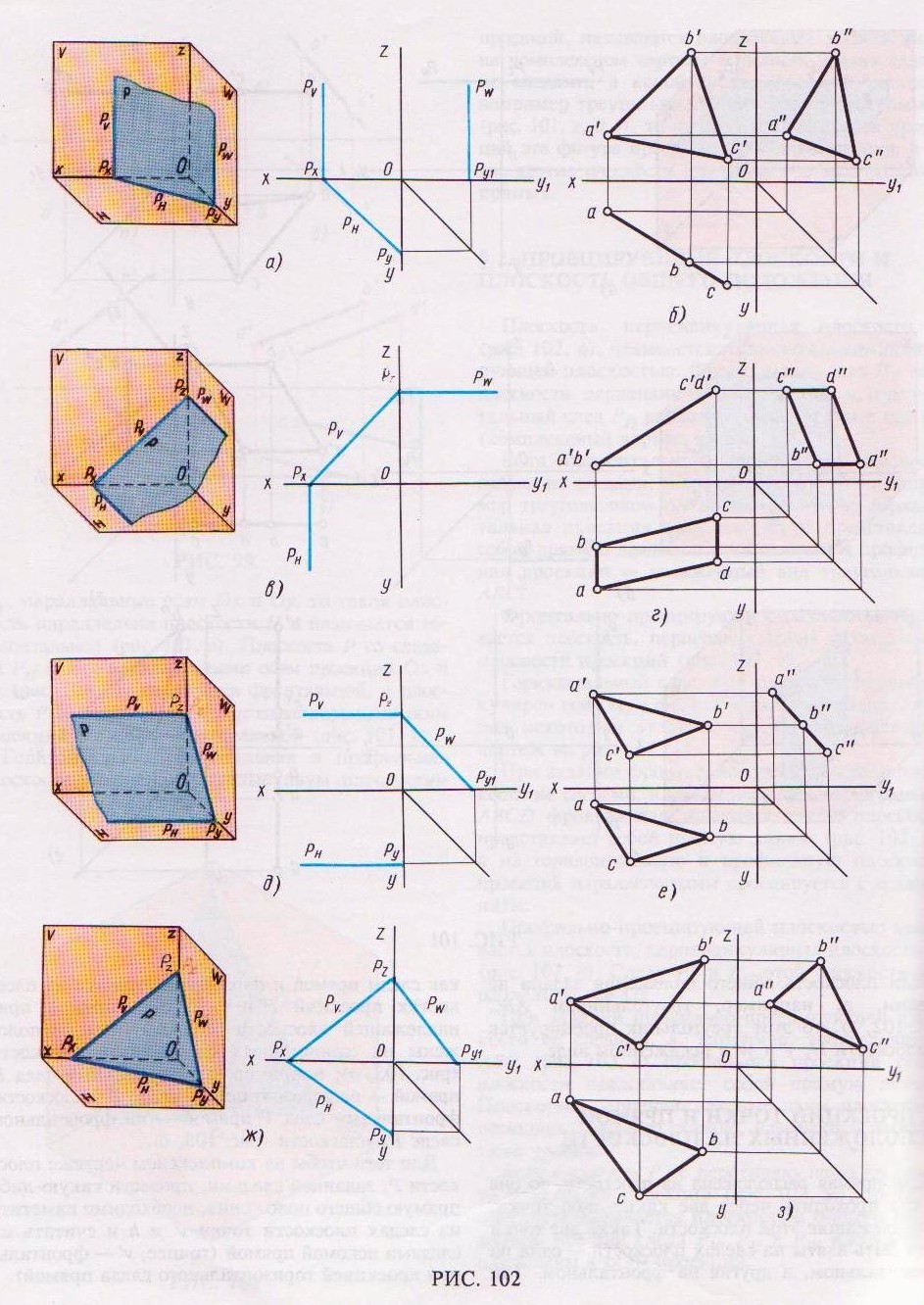
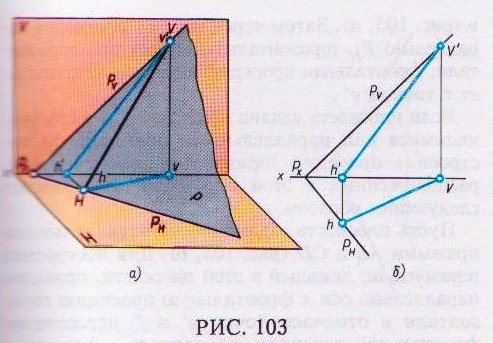
Опустив перпендикуляры из v' и h на ось проекций х. находим на ней вторые проекции следов прямой: ν – горизонтальную проекцию фронтального следа прямой и h – фронтальную проекцию горизонтального следа прямой. Соединив одноименные проекции следов, т.е. ν ´ с h´ и v с h прямыми, получим две проекции прямой линии, расположеннойв плоскости общего положения Р.

Очень часто требуется провести на плоскости горизонталь и фронталь, которые называются линиями уровня плоскости. Главные линии помогают решать многие задачи проекционного черчения.

Горизонталь и фронталь имеют в системе двух плоскостей V и Н только по одному следу (например горизонталь имеет только фронтальный след). Поэтому, зная один след линии уровня, проекцию этой линии проводят по заранее известному направлению. Это направление для горизонтали видно из рис. 104, а, где показана плоскость общего положения и горизонталь, лежащая на ней. Из рисунка видно, что горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

Таким образом, чтобы на комплексном чертеже плоскости P провести в этой плоскости какую-либо горизонталь, нужно наметить на следе P_V плоскости точку v ' (рис. 104, б) и считать ее фронтальной проекцией фронтального следа горизонтали. Затем через точку v' параллельно оси х проводят прямую, которая будет фронтальной проекцией горизонтали.

Опустив перпендикуляр из точки v ' на ось x, получают точку v, которая будет горизон­тальной проекцией фронтального следа горизонтали. Прямая, проведенная из точки v параллельно следу Р_Hплоскости, представляет собой горизонтальную проекцию искомой горизонтали. Построение проекции фронтали показано на рис. 104, в и г.

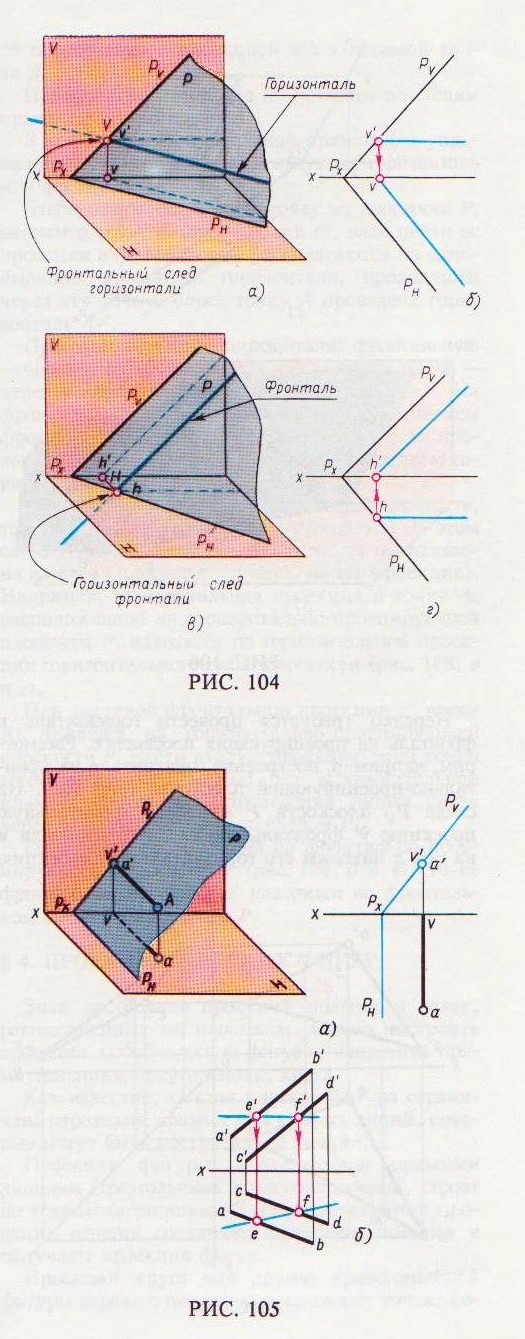
Нередко требуется провести горизонталь и фронталь на проецирующих плоскостях. Рассмот­рим, например, построение горизонтали на фрон­тально-проецирующей плоскости (рис. 105). На следе Рv плоскости Р намечаем фронтальную проекцию v' фронтального следа горизонтали и на оси х находим его горизонтальную проекцию

v (рис. 105, а). Затем через точку v проводим па­раллельно Р_H горизонтальную проекцию горизон­тали; фронтальная проекция горизонтали совпада­ет с точкой v'.

Если плоскость задана не следами, а пересека­ющимися или параллельными прямыми, то по­строение проекций горизонтали или фронта расположенных в этой плоскости, выполняется следующим образом.

Пусть плоскость задана двумя параллельными
прямыми АВ и CD (рис. 105, б). Для построен
горизонтали, лежащей в этой плоскости, проводим
параллельно оси х фронтальную проекцию гори­зонтали и отмечаем точки е' и f ' пересечение
фронтальной проекции горизонтали с фронтальными проекциями параллельных прямых, которыми задана плоскость. Через точки е' и f ' прово­дим вертикальные линии связи до пересечения ab и cd в точках е и f. Точки е и f соединяем прямой линией, которая и будет горизонтальной проекцией горизонтали.

Если требуется найти следы плоскости, зад ной пересекающимися или параллельными прямыми, надо найти следы этих прямых и через полученные точки провести искомые следы плоскости.

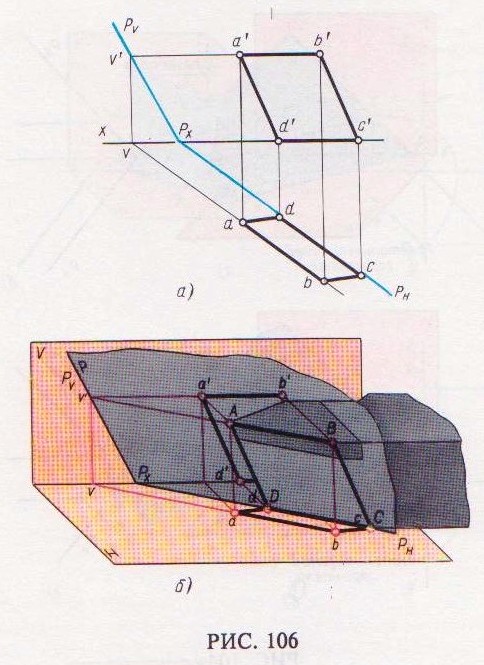
Рассмотрим комплексный чертеж параллелограмма ABCD (рис. 106, а), который задает некоторую плоскость ABCD. Отрезок DC расположен в плоскости Н, следовательно, его горизонтальная проекция dc является горизонтальным следом плоскости или горизонтальной проекцией горизонтального следа плоскости.

Чтобы найти фронтальный след этой плоскости, необходимо продолжить горизонтальную проекцию dc прямой DC до пересечения с осью точке Р_х, через которую должен пройти искомый фронтальный след плоскости.

Второй точкой v ', через которую пройдет искомый фронтальный след плоскости, является фронтальный след прямой АВ (фронтальная проекция фронтального следа). Фронтальную проекция фронтального следа прямой АВ находим, продолжая горизонтальную проекцию ab прямой АВ до пересечения с осью х в точке v, которая будет горизонтальной проекцией искомого фронтального следа прямой АВ. Фронтальная проекция фронтального следа этой прямой находится на перпендикуляре, восстановленном из точки v оси х, в точке v ' его пересечения с продолжением фронтальной проекции а'b' прямой АВ. Соединив точки Р_х с v ', находим фронтальный след Р_V плоскости.

Пример решения подобной задачи приведен на рис 106, б.

Часто на комплексных чертежах приходится решать такую задачу: по одной из заданных проек-

ций точки расположенной на заданной плоскости, определить две другие проекции точки.

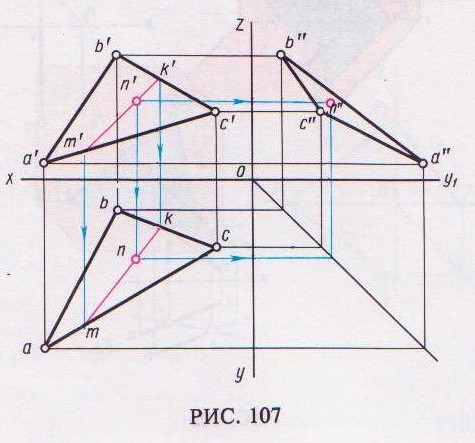
Через заданную проекцию точки, например, фронтальную проекцию п' точки N, расположенной на плоскости треугольника ABC (рис. 107), проводим одноименную проекцию вспомогательной прямой любого направления, например, т'к'. Строим другую проекцию тк вспомогательной прямой. Для этого проводим вертикальные линии

связи через точки т ' и к' до пересечения с линиями ас и bс. Из точки п' проводим линию связи

до пересечения с проекцией тк в искомой точ­ке п.

Профильную проекцию п" находим по общим правилам проецирования.

В качестве вспомогательной прямой для упро­щения построения чаще используются горизонталь или фронталь.

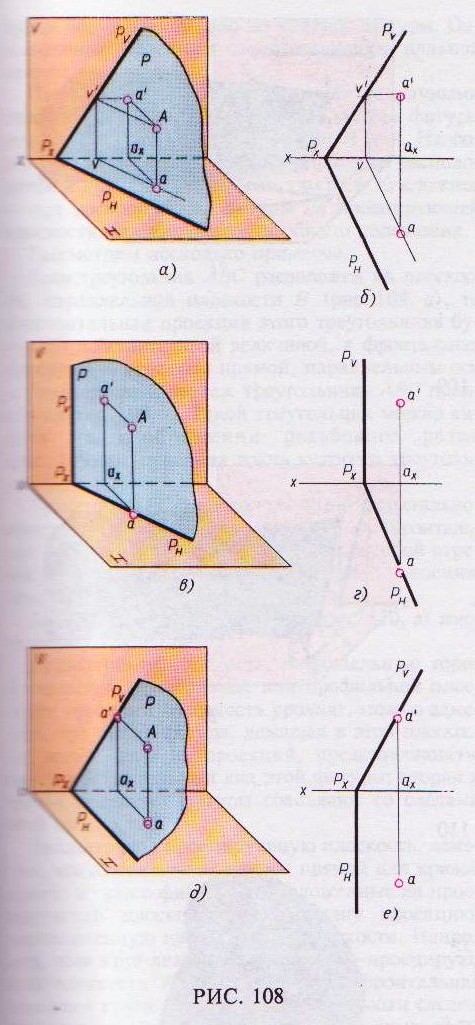
Чтобы найти какую-либо точку на плоскости Р, например точку А (рис. 108, а и б), надо найти ее проекции а' и а, которые располагаются на одно­именных проекциях горизонтали, проходящей через эту точку. Через точку А проведена гори­зонталь Av'.

Проводим проекции горизонтали: фронтальную – через v' параллельно оси х, горизонтальную – через v параллельно следу Р_н плоскости Р. На фронтальной проекции горизонтали намечаем фронтальную проекцию а' искомой точки и, про­водя вертикальную линию связи, определяем го­ризонтальную проекцию а точки А.

Если точка лежит на проецирующей плоскости, то построение ее проекций упрощается. В этом случае одна из проекций точки всегда расположе­на на следу плоскости (точнее, на его проекции). Например, горизонтальная проекция а точки А, расположенной на горизонтально-проецирующей плоскости Р, находится на горизонтальной проек­ции горизонтального следа плоскости (рис. 108, в и г).

При заданной фронтальной проекции а' точки А, лежащей на горизонтально-проецирующей плоскости Р, найти вторую проекцию этой точки (горизонтальную) можно без вспомогательной прямой, посредством проведения линии связи через а' до пересечения со следом Р_Н.

Если точка расположена на фронтально-прое­цирующей плоскости Р (рис. 108, д и е), то ее фронтальная проекция а' находится на фронталь­ном следе Р _vплоскости Р.