Проекции плоских фигур

Зная построение проекций прямых и точек, расположенных на плоскости, можно построить проекции любой плоской фигуры, например, пря­моугольника, треугольника, круга.

Как известно, каждая плоская фигура ограни­чена отрезками прямых или кривых линий, кото­рые могут быть построены по точкам.

Проекции фигуры, ограниченной прямыми линиями (треугольника и многоугольника), строят по точкам (вершинам). Затем одноименные про­екции вершин соединяют прямыми линиями и получают проекции фигур.

Проекции круга или другой криволинейной фигуры строят с помощью нескольких точек, ко-

торые берут равномерно по контуру фигуры. Одноименные проекции точек соединяют плавной кривой по лекалу.

Проекции плоской фигуры строят различными способами в зависимости от положения фигуры относительно плоскостей проекций Н и V. Наибо­лее просто построить проекции фигуры, располо­женной параллельно плоскостям Н и V; сложнее - при расположении фигуры на проецирующей плоскости или на плоскости общего положения.

Рассмотрим несколько примеров.

Если треугольник ABC расположен на плоскости, параллельной плоскости Н (рис. 109, а), то

горизонтальная проекция этого треугольника будет его действительной величиной, а фронтальная

проекция – отрезком прямой, параллельным оси х. Комплексный чертеж треугольника ABC показан на рис. 109. б. Такой треугольник можно видеть на изображении резьбового резца рис. (109, в), передняя грань которого треугольная.

Трапеция ABCD расположена на фронтально-проецирующей плоскости (рис. 110, а). Фронтальнаяпроекция трапеции представляет собой отрезок прямой линии, а горизонтальная –трапецию (рис. 110, б).

Задняя грань отрезного резца (рис. 110, в) имеет форму трапеции.

Рассматривая плоскость, параллельную горизонтальной, фронтальной или профильной плоскости проекций (плоскость уровня), можно заметить, что любая фигура, лежащая в этой плоскости, имеет одну из проекций, представляющую собой действительный вид этой фигуры; вторая и третья проекции фигуры совпадают со следами этой плоскости.

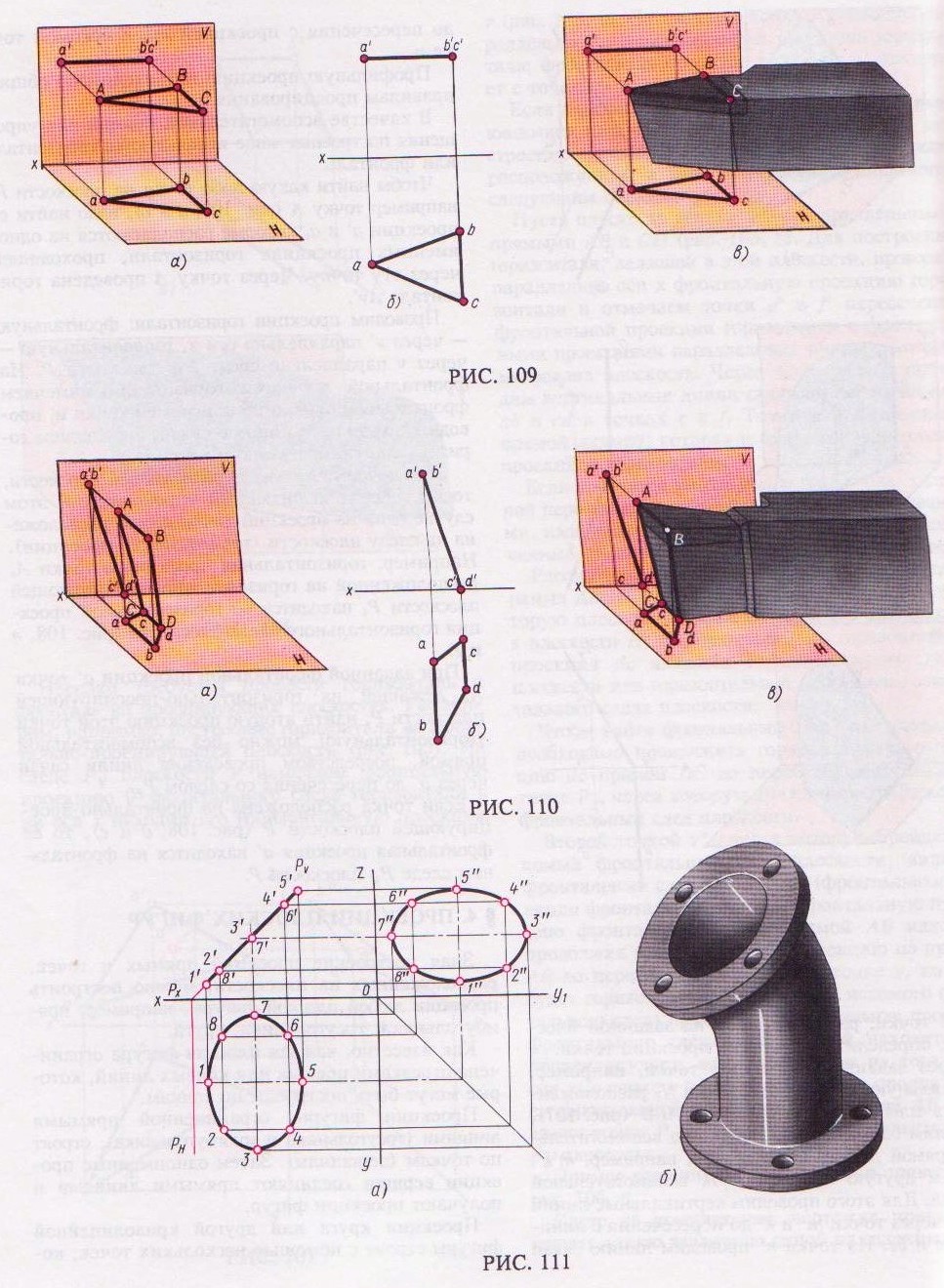
Рассматривая проецирующую плоскость, заметим, что любая точка, отрезок прямой или кривой линии, а также фигуры, расположенные на проецирующей плоскости, имеют одну проекцию, расположенную на следе этой плоскости. Например, если круг лежит на фронтально-проецирующей плоскости Р (рис. 111, а), то фронтальная проекциякруга совпадает с фронтальным следом Р_V плоскости Р.Две другие проекции круга искажены и представляют собой эллипсы. Большие оси эллипсов равны проекциям диаметра круга 37. Малые оси эллипсов равны проекциям диаметра круга 15, перпендикулярного диаметру круга 37. Остальные точки проекций эллипса определяются следующим образом. Вспомогательная полуокружность делится на четыре равные части, методом проецирования определяются остальные проекции точек 2, 8, 4, 6.

На рис. 111, б показано колено трубы с двумя фланцами. Горизонтальная проекция контура нижнего фланца, который расположен в горизонтальной плоскости, будет действительным видом окружности. Горизонтальная проекция контура верхнего фланца изобразится в виде эллипса.

§ 5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Две плоскости могут быть взаимно параллель­ными или пересекающимися.

Из стереометрии известно, что если две парал­лельные плоскости пересекают какую-либо третью плоскость, то линии пересечения этих плоскостей параллельны между собой. Исходя из этого поло­жения, можно сделать вывод, что одноименные следы двух параллельных плоскостей Р и Q также параллельны между собой.

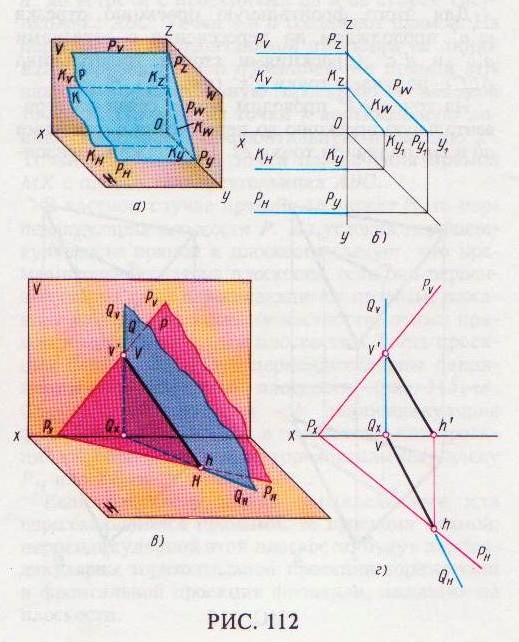
Если равны две профильно-проецирующие пло­скости Р и К (рис. 112, а), то параллельность их фронтальных и горизонтальных следов на ком­плексном чертеже в системе V и Н недостаточна для того, чтобы определить, параллельны эти плоскости или нет. Для этого необходимо постро­ить их профильные следы в системе V, Н и W (рис. 112, б). Плоскости Р и К будут параллельны только в том случае, если параллельны их про­фильные следы Р_W, и K_W.

Одноименные следы пересекающихся плоскос­тей Р и Q (рис. 112, в) пересекаются в точках V

и Н, которые принадлежат обеим плоскостям, т.е. линии их пересечения. Так как эти точки распо­ложены на плоскостях проекций, то, следователь­но, они являются также следами линии пересече­ния плоскостей. Чтобы на комплексном чертеже построить проекции линии пересечения двух плоскостей Р и Q, заданных следами P_w, P_H и Q_V, необходимо отметить точки пересечения одно­именных следов плоскостей, т.е. точки v' и h (рис. 112, г); точка v' – фронтальная проекция фронтального следа искомой линии пересечения плоскостей Р и Q, h - горизонтальная проекция горизонтального следа этой же прямой. Опуская перпендикуляры из точек v' и h на ось х, нахо­дим точки V и h. ' Соединив прямыми одноименные проекции следов, т.е. точки v' и h ', v и h, полу­чим проекции линии пересечения плоскостей P и Q