
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция распределения вероятностей случайной величины и ее свойства.
|
|
Рассмотрим функцию F(х), определенную на всей числовой оси следующим образом: для каждого х значение F(х) равно вероятности того, что дискретная случайная величина 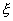 примет значение, меньшее х, т. е.
примет значение, меньшее х, т. е.
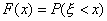
| (18) |
Эта функция называется функцией распределения вероятностей, или кратко, функцией распределения.
пример 1. Найти функцию распределения случайной величины 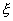 , приведенной в примере 1, п. 1.
, приведенной в примере 1, п. 1.
Решение: Ясно, что если 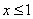 , то F(x)=0, так как
, то F(x)=0, так как 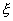 не принимает значений, меньших единицы. Если
не принимает значений, меньших единицы. Если  , то
, то 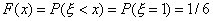 ; если
; если 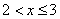 , то
, то 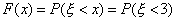 . Но событие
. Но событие 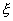 < 3 в данном случае является суммой двух несовместных событий:
< 3 в данном случае является суммой двух несовместных событий: 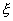 =1 и
=1 и 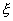 =2. Следовательно,
=2. Следовательно,
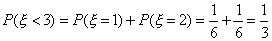
Итак для 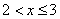 имеем F(x)=1/3. Аналогично вычисляются значения функции в промежудках
имеем F(x)=1/3. Аналогично вычисляются значения функции в промежудках 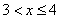 ,
, 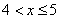 и
и 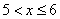 . Наконец, если x> 6 то F(x)=1, так как в этом случае любое возможное значение
. Наконец, если x> 6 то F(x)=1, так как в этом случае любое возможное значение 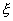 (1, 2, 3, 4, 5, 6) меньше, чем x. График функции F(x) изображен на рис. 4.
(1, 2, 3, 4, 5, 6) меньше, чем x. График функции F(x) изображен на рис. 4.
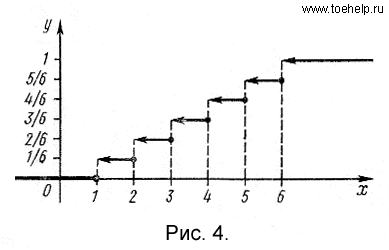
Пример 2. Найти функцию распределения случайной величины  , приведенной в примере 2, п. 1.
, приведенной в примере 2, п. 1.
Решение: Очевидно, что
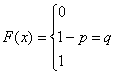
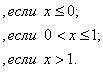
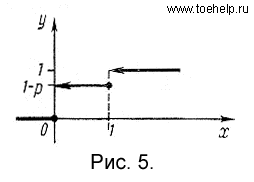
График F(x) изображен на рис. 5.
Зная функцию распределения F(x), легко найти вероятность того, что случайная величина 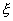 удовлетворяет неравенствам
удовлетворяет неравенствам 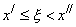 .
.
Рассмотрим событие, заключающееся в том, что случайняя величина примет значение, меньшее 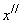 . Это событие распадается на сумму двух несовместных событий: 1) случайная величина
. Это событие распадается на сумму двух несовместных событий: 1) случайная величина 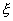 принимает значения, меньшие
принимает значения, меньшие 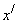 , т.е.
, т.е. 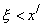 ; 2) случайная величина
; 2) случайная величина 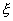 принимает значения, удовлетворяющие неравенствам
принимает значения, удовлетворяющие неравенствам 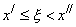 . Используя аксиому сложения, получаем
. Используя аксиому сложения, получаем
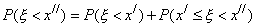
Отсюда
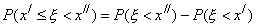
Но по определению функции распределения F(x) [см. формулу (18)], имеем 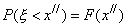 ,
, 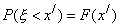 ; cледовательно,
; cледовательно,
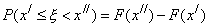
| (19) |
Таким образом, вероятность попадания дискретной случайной величины в интервал 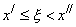 равна приращению функции распределения на этом интервале.
равна приращению функции распределения на этом интервале.
Рассмотрим основные свойства функции распределения.
1°. Функция распределения является неубывающей.
В самом деле, пусть 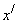 <
< 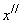 . Так как вероятность любого события неотрицательна, то
. Так как вероятность любого события неотрицательна, то 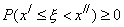 . Поэтому из формулы (19) следует, что
. Поэтому из формулы (19) следует, что 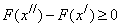 , т.е.
, т.е. 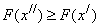 .
.
2°. Значения функции распределения удовлетворяют неравенствам 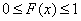 .
.
Это свойство вытекает из того, что F(x) определяется как вероятность [см. формулу (18)]. Ясно, что * 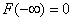 и
и 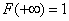 .
.
3°. Вероятность того, что дискретная случайная величина 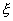 примет одно из возможных значений xi, равна скачку функции распределения в точке xi.
примет одно из возможных значений xi, равна скачку функции распределения в точке xi.
Действительно, пусть xi - значение, принимаемое дискретной случайной величиной, и 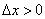 . Полагая в формуле (19)
. Полагая в формуле (19) 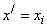 ,
, 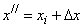 , получим
, получим
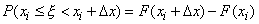
| (20) |
В пределе при 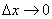 вместо вероятности попадания случайной величины на интервал
вместо вероятности попадания случайной величины на интервал 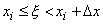 получим вероятность того, что величина
получим вероятность того, что величина 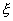 примет данное значение xi:
примет данное значение xi:
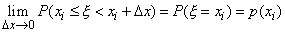
C другой стороны, получаем 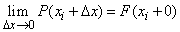 , т.е. предел функции F(x) справа, так как
, т.е. предел функции F(x) справа, так как 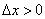 . Следовательно, в пределе формула (20) примет вид
. Следовательно, в пределе формула (20) примет вид
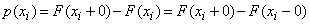
| (21) |
т.е. значение p(xi) равно скачку функции ** xi. Это свойство наглядно иллюстрируется на рис. 4 и рис. 5.