Равномерное распределение.

Пусть сегмент [a, b] оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина 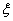могущая принять любое значение из сегмента [a, b]. Поэтому 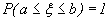. Если, далее, x1 и x2 (x1< x2) - две любые отметки на шкале, то согласно условию имеем

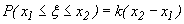
где k - коэффициент пропорциональности, не зависящий от x1 и x2, а разность x2-x1, - длина сегмента [x1, x2]. Так как при x1=a и x2=b имеем 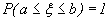, то k(b-a)=1, откуда k=1/(b-a). Таким образом

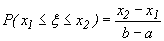
(26)

Теперь легко найти функцию F(x) распределения вероятностей случайной величины 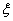. Если 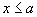, то 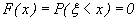так как 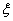не принимает значений, меньших a. Пусть теперь 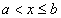. По аксиоме сложения вероятностей 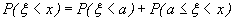. Согласно формуле (26), в которой принимаем x1=a, x2=х имеем

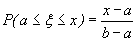
Так как 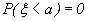, то при 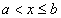получаем

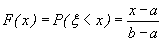
Наконец, если x> b, то F(x)=1, так как значения 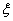лежит на сегменте [a, b] и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения:

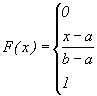
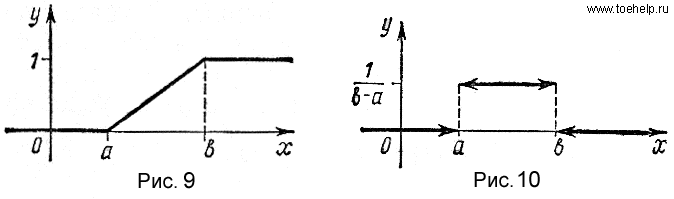
График функции F(x) представлен на рис. 9.

Плотность распределения вероятностей найдем по формуле (25). Если x< a или x> b, то 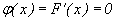. Если a< x< b, то

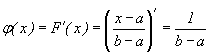
Таким образом,

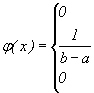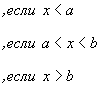
(27)

График функции 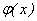изображен на рис. 10. Заметим, что в точках a и b функция 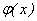терпит разрыв.

Величина, плотность распределения которой задана формулой (27), называется равномерно распределенной случайной величиной.